Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Stirlingova čísla a padající faktoriály (TOTO TÉMA JE VYŘEŠENÉ)
#1 18. 02. 2011 02:04 — Editoval FailED (03. 11. 2011 20:30)
Stirlingova čísla a padající faktoriály
Přidávám jednu úlohu kterou jsme jednou dostali na cvičení z diskrétky:
Dokažte, že pro  platí
platí
kde  je padající faktoriál a
je padající faktoriál a  je S(n,k) - Stirlingovo číslo druhého druhu (počet ekvivalencí na n-prvkové množině s k třídami).
je S(n,k) - Stirlingovo číslo druhého druhu (počet ekvivalencí na n-prvkové množině s k třídami).
Offline
- (téma jako vyřešené označil(a) FailED)
#2 18. 02. 2011 16:56
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Stirlingova čísla a padající faktoriály
↑ FailED:
Berete tzv. "diskrétní kalkulus" - analogii integrování pro sumy?
"Máte úhel beta." "No to nemám."
Offline
#3 18. 02. 2011 17:05 — Editoval FailED (18. 02. 2011 23:45)
Re: Stirlingova čísla a padající faktoriály
↑ check_drummer:
Dělali jsme součty  a jeden způsob získání obecného vzorce využívá právě tohle.
a jeden způsob získání obecného vzorce využívá právě tohle.
Cvičící nám k tomu dokonce napsal pohádku kde se o diskrétním kalkulu taky zmínil.
Offline
#4 20. 09. 2011 16:11 — Editoval FailED (03. 11. 2011 20:32)
Re: Stirlingova čísla a padající faktoriály
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Stirlingova čísla a padající faktoriály (TOTO TÉMA JE VYŘEŠENÉ)

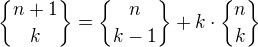 .
.