Matematické Fórum

check_drummer · 22. 07. 2011 19:01

Ahoj,
z prvočíselné věty plyne (zhruba řečeno), že pravděpodobnost, že nějaké "velké" číslo n je prvočíslo, je 1/ln(n).

Lze nějakým způsobem odvodit nebo je známo, jaká je pravděpodobnost (opět "limitně" pro nějaké "velké" n), že mezi čísly n-k až n+k (kde k je pevné) jsou alespoň dvě prvočísla? Dle mého nelze "násobení" pravděpodobností použít, protože výskyt dvou prvočísel (a zvlášť blízko sebe) není (IMHOtep) nezávisílý.

Otázka je, jak toto vůbec zformalizovat. Můj návrh je pro dané n určit, jaká četnost "dobrých" n (tj. s aspoň dvěma prvočísly ve svém okolí) je mezi n a m (m>n) a toto číslo označit p(n,m,k), následně najít nějakou "limitní" (asymptotickou) funkci f(n,m,k), která je nějak "pěkně" analyticky popsaná (podobně jako n/log(n) u prvočíselné věty), tj. takovou, že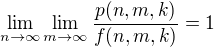
$\lim_{n \to \infty}\lim_{m \to \infty}\frac{p(n,m,k)}{f(n,m,k)} = 1$ .
Pak je hledaný odhad pravděpodobnosti pro dané n dle mého roven f(n,1,k).

Zajímal by mě názor někoho dalšího na tuto věc. Díky za něj.

FailED · 19. 09. 2011 23:38 — Editoval FailED (19. 09. 2011 23:41)

Ahoj,

myslím, že to známo není, alespoň pro k=1 by to řešilo otevřený problém prvočíselných dvojčat, o kterých se ani neví, jestli je jich nekonečno.

Nedávno jsem narazil na (populárně naučnou) přednášku. Ke konci tam Terrence mluví o některých novějších výsledcích a otevřených problémech týkajících se prvočísel, možná tam najdeš i odpověď na svoji otázku.

check_drummer · 20. 09. 2011 16:50

↑ FailED:
Řešilo by to problém pouze v tom, případě, že by uvedená pravděpodobnost vyšla nenulová. Pokud by byla nulová, tak dle mého by těchto dvojčat mohlo být nekonečně mnoho, pokud by byla rozmístěna dostatečně "řídce". Což je celkem zajímavé téma, možná zformuluju nějakou zajímavou úlohu. :-)
Díky za odkaz, pokud najdu čas, podívám se.

FailED · 20. 09. 2011 17:22 — Editoval FailED (20. 09. 2011 17:59)

↑ check_drummer:

Jestli to dobře chápu, kdyby funkce f(n,m,k) splňovala tu limitu, musela by být p(n,m,k) nenulová pro každé velké n a k němu dost velké m. (protože i f(n,m,k) se pro velké n a m nesmí rovnat nule)

Asi jsem to napsal špatně, existence f(n,m,1) podle mě implikuje nekonečno prvočíselných dvojčat.

check_drummer · 20. 09. 2011 21:24

↑ FailED:
Takhle na první pohled myslím, že kdyby bylo třeba $f(n,m,k) = \sqrt{m-n}$ , že by uvedená pravděpodobnost byla 0. Ale úplně hluboko jsem nad tím nepřemýšlel, nechám si to na zítra.

vanok · 03. 10. 2011 16:57

ahoj Check_,

Mas zaujimave myslienky ak dokazes tvoju teoremu daj nam vediet

Inac na pre cvicenie mozes porozmyslal sice o jednoduchsom probleme: Bertrand's postulate

Pozri aj na

http://cs.wikipedia.org/wiki/Bertrand%C … tul%C3%A1t

Skus najst sam riesenie alebo ak nemas na to cas pozri na priklad na

http://en.wikipedia.org/wiki/Bertrand%27s_postulate

Srdecne

Vanok

Matematické Fórum

#1 22. 07. 2011 19:01

Pravděpodobnost, že v okolí prvočísla existuje prvočíslo

#2 19. 09. 2011 23:38 — Editoval FailED (19. 09. 2011 23:41)

Re: Pravděpodobnost, že v okolí prvočísla existuje prvočíslo

#3 20. 09. 2011 16:50

Re: Pravděpodobnost, že v okolí prvočísla existuje prvočíslo

#4 20. 09. 2011 17:22 — Editoval FailED (20. 09. 2011 17:59)

Re: Pravděpodobnost, že v okolí prvočísla existuje prvočíslo

#5 20. 09. 2011 21:24

Re: Pravděpodobnost, že v okolí prvočísla existuje prvočíslo

#6 03. 10. 2011 16:57

Re: Pravděpodobnost, že v okolí prvočísla existuje prvočíslo

Zápatí