Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 09. 2011 19:12
arcsin pomocí +,-*,/
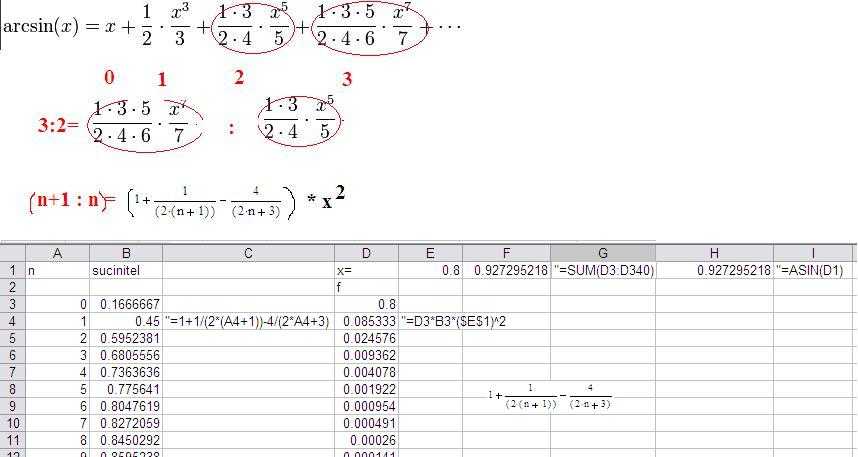
Ahojte. Chci zapsat arcsin, ale jen pomocí +,-,*,/. Našel jsem si na Wikipedii Taylorovu řadu, ověřil jsem si to v "BARTSCH Matematicke vzorce". Teď bádám nad tím, jak zapíši mocninu. Našel jsem způsob, jak zapíši pouze druhou mocninu pomocí sčítání.
Mám rozepsané na papíře několik možností, ale ani z jedné mi nic nevychází. Mohli by jste mě nasměrovat? Možná, že bych rád zavedl i nějakou heuristiku, pokud by to nebylo nad moje chápání. Děkuji.
Offline
#2 21. 09. 2011 19:21
Re: arcsin pomocí +,-*,/
↑ Tomaskocz:
Já jsem asi hloupej, ale nějak jsem nepochopil co potřebuješ. Co se ti na té Taylorově řadě nelíbí (kromě toho že místo toho z má být x)?
Pokud chceš zapsat mocninu pomocí + - * /, doporučuji dělat to pomocí násobení, např. 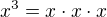 , ale to předpokládám nebude to cos chtěl.
, ale to předpokládám nebude to cos chtěl.
Offline
#3 21. 09. 2011 19:24
Re: arcsin pomocí +,-*,/
Vzorec je správně.
1. Zadáváš proměnou [x] v radiánech, to znamená 45° je pi/4, tj. 0.7853981633974483
2. Přesnost vzorce je omezená, od 0 do pi/4 je vynikající, pak rapidně klesá (musíš použít buď vyšší stupeň, což je velmi nevýhodné, nebo počítat jakoby z "druhé strany")
Offline
#5 21. 09. 2011 22:08 — Editoval Oxyd (21. 09. 2011 22:44)
Re: arcsin pomocí +,-*,/
↑ Tomaskocz:
Předpokládám, že to nechceš vyhodnocovat jako řadu, ale jenom jako polynom nějakého stupně (tzn. chceš aproximaci) a chceš se při tom vyhnout neustálému počítání k-tých mocnin, že?
Normálně bych to převedl pomocí Hornerova schématu. Tzn. vytýkal bych x^2. Nějak takhle:
Při vyhodnocování posledního výrazu ti stačí znát jenom x a x^2 (které si můžeš předpočítat) -- pak to vyhodnocovat postupně „zevnitř“ -- nejdřív závorku s x/7, tu přenásobit x^2, přičíst to s x/5, vynásobit x^2, přičíst to s x/3, vynásobit x^2, přičíst x, hotovo.
Edit: A ještě víc se toho dá vytknout:
Snad si dovedeš představit algoritmus, který pro zadaný stupeň a x podle tohohle schématu rovnou vyhodnotí tenhl epolynom v bodě x.
A ano, snad by byla lepší sekce Algoritmy a programování, aby bylo jasnější, že to chceš programovat. Však on to tam někdo přesune.
Edit 2:
mák napsal(a):
Vzorec je správně.
1. Zadáváš proměnou [x] v radiánech, to znamená 45° je pi/4, tj. 0.7853981633974483
2. Přesnost vzorce je omezená, od 0 do pi/4 je vynikající, pak rapidně klesá (musíš použít buď vyšší stupeň, což je velmi nevýhodné, nebo počítat jakoby z "druhé strany")
Nepleteš si arcsin se sin? Parametr funkce arcsin je reálné číslo od -1 do 1, jeho výsledek je nějaký úhel měřený v radiánech.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#7 24. 09. 2011 12:05
Re: arcsin pomocí +,-*,/
Už to mám naprogramované. Např. pro číslo 0.5 pro 10 platných cifer se mi cyklus provede 13x pro 0.8 se cyklus provede už 40x a pro číslo 1 se cyklus provede 9266873x a už to číslo není vůbec přesné.
Chci tedy předtím než začne výpočet u čísel menších než -0.5 a větších než 0.5 je dát do rozsahu <-0.5 ; 0.5> a pak to nějakým mechanismem převést zpátky, aby číslo vyšlo správě. Udělat optimalizaci, protože výpočet probíhá snadněji pro čísla z mého definovaného intervalu <-0.5 ; 0.5>.
Offline
#12 24. 09. 2011 13:25
Re: arcsin pomocí +,-*,/
Pokud Taylorův rozvoj pro arcsin rozvinu blíž např. v okolí bodu 0.5, tak jak z něj dostanu např arcsin 0,9 nebo arsin 0,987?
Do toho polynomu dosadíš úplně stejně jako když ho rozvíjíš v 0.
Offline
#13 24. 09. 2011 13:33
Re: arcsin pomocí +,-*,/
FailED napsal(a):
Pokud Taylorův rozvoj pro arcsin rozvinu blíž např. v okolí bodu 0.5, tak jak z něj dostanu např arcsin 0,9 nebo arsin 0,987?
Do toho polynomu dosadíš úplně stejně jako když ho rozvíjíš v 0.
To vím, ale mě jde o to že když tam dosadím 0,9, tak ten rozvoj je strašně dlouhý, než dosáhnu požadované přesnosti. Když chci spočítat např. arcsin 0,9, tak ho potřebuji spočítat v menších číslech např. arcsin 0,5 aby rozvoj nebyl tak dlouhý, a pak to třeba vynásobit do arcsin 0,9 nebo nasčítat nebo něco...zkrátka udělat heuristiku. Nevím jak to mám říct, možná to říkám zle :/
Offline
#14 24. 09. 2011 14:33 — Editoval FailED (24. 09. 2011 14:54)
Re: arcsin pomocí +,-*,/
Proto navrhuji arcsin x pro x z (0.5, 1] počítat pomocí taylorova rozvoje v ↑ sqrt(3)/2:, který tu funkci na tom intervalu aproximuje mnohem líp.
Nevím, jestli existují nějaké užitečné identity pro arcsin.
Sám nevím, jak se arcsin x normálně počítá, zkusil bych numericky řešit rovnici siny-x=0. (pro y, třeba Newtonovou metodou) Sinus má totiž omezené derivace, proto pro něj taylor funguje mnohem líp. Navíc se dají výhodně použít součtové vzorce.
Offline
#15 25. 09. 2011 21:57
Re: arcsin pomocí +,-*,/
Ahojte, skúsil som takto..
a celkom to sedí v Exceli, ale asi aj v iných cykloch..
Offline
#18 30. 09. 2011 14:22
Re: arcsin pomocí +,-*,/
↑ Tomaskocz:
To opravdu ne.
Zkus si spočítat, pro nějaké hodně velké n (např. 1000000000) kolik ti vyjde arcsin(x):
Podle tebe to bude:
arcsin(x)=0.999999999x^2 (což je skoro x^2-dost přesně) a to jistě pro obecné x není pravda
Offline
#20 05. 11. 2011 16:07
Re: arcsin pomocí +,-*,/
↑ Tomaskocz: kdybys neignoroval ↑ FailEDovy: rady, už jsi to mohl mít
Offline
#22 06. 11. 2011 12:04
Re: arcsin pomocí +,-*,/
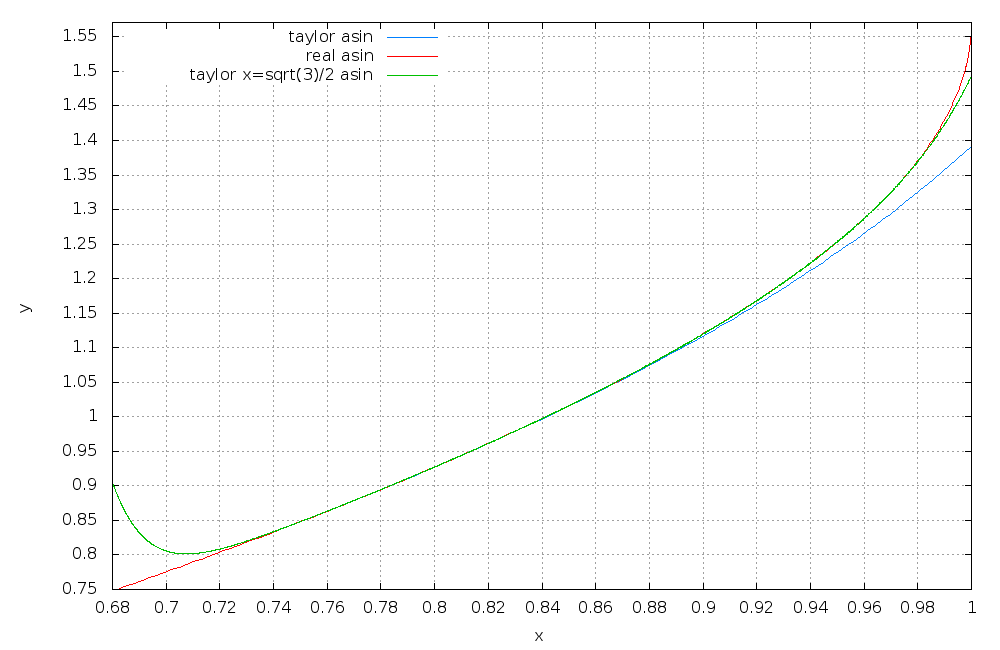
Dole máš obrázek.
Skutečný průběh funkce arcsin je v červené barvě.
Tebou aproximovaný průběh je v modré barvě (vlevo se kryje s červenou, takže není vidět, napravo se odchyluje od skutečnosti).
Pokud rozvineš taylora například u sqrt(3)/2, pak budeš mít průběh podle zelené barvy, který lépe aproximuje funkci při vyšších hodnotách.
Offline
#23 06. 11. 2011 15:33 — Editoval .pata. (06. 11. 2011 18:11)
Re: arcsin pomocí +,-*,/
A víte někdo jak roste ta řada? Podle odkazu na wolframalpha, by to šlo pěkně udělat, jen víte někdo jak roste to číslo před závorkou? Čím ho násobit, co k němu přičíst atd.? Aby z toho šlo udělat cyklus, který v každém opakování to číslo o něco zvětší a nevím to něco, čím to zvětšit. Pak by to bylo skvělé řešení, ale jinak to nejde implementovat do cyklu.
EDIT: Jde to tak, že pro různé intarvaly použiješ různé řady. S minimálním počtem iterací ;) Stačí hledat a testovat, papír a tužka jako vždy nejlepší.
Offline