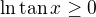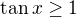Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 09. 2011 20:41
Definiční obory goniometrických fcí
Ahoj, prosímvás poradíte mi někdo s těmito funkcemi ? Nemůžu přijít na to jak udělat Df...nebo respektive znám podmínky které mám řešit, ale nevím jak je vyřešit. Domácí cvičení jedná se o část Definiční obory a grafy funkcí - příklad 1L) a 1N) klasicky urcim podmínky, že vyrazy pod odmocninou musi byt vetsi nebo rovny 0. A to už mi nejde vyřešit :/
Offline
#2 26. 09. 2011 20:50
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Definiční obory goniometrických fcí
↑ vviston:
Když vezmu třeba příklad M), tak pro arcus kosinus platí, že je definován na intervalu <-1; 1>. To znamená, že stačí vyřešit nerovnici 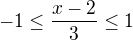 .
.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#3 26. 09. 2011 20:55
Re: Definiční obory goniometrických fcí
↑ Aquabellla: jojo, ten byl jednoduchej, ale zbyle goniometricke funkce nevim jak doresit...
Offline
#4 26. 09. 2011 21:00
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Definiční obory goniometrických fcí
↑ vviston:
jo aha, pardon, já četla, že nevíš 1L) až 1N) :-)
1L:
Urči podmínky zvlášť pro každou z těch odmocnin a poté udělej průnik těch dvou mezi-řešení.
Doporučuji si namalovat graf a z toho určit, kdy je daný sinus větší nebo rovno nula (odmocninu nelze udělat ze záporného čísla)
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#5 26. 09. 2011 21:05
Offline
#6 26. 09. 2011 22:13
Re: Definiční obory goniometrických fcí
↑ zdenek1: No a ja prave nevim jak vyresit tg x >= 1 proste tuhle nerovnici nedám at chci nebo ne...u toho jsem se zasekl :/
Offline
#7 26. 09. 2011 22:24
#8 26. 09. 2011 22:28
Re: Definiční obory goniometrických fcí
↑ vviston:
Tady asi nezbývá než zopakovat radu ↑ Aquabellla:. Nejlepší je mít v hlavě grafy goniometrických funkcí.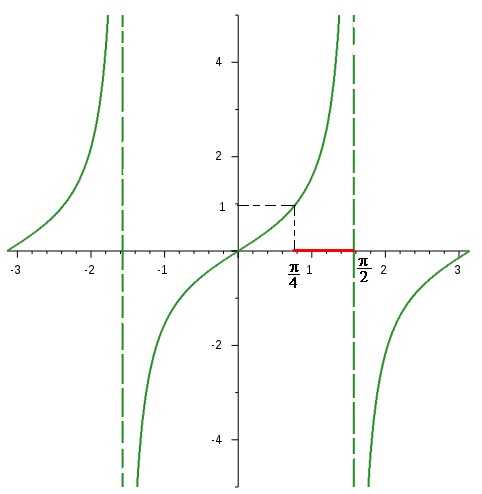
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#10 26. 09. 2011 22:38 — Editoval ((:-)) (26. 09. 2011 22:39)
Re: Definiční obory goniometrických fcí
↑ vviston:
Funkcia tangens uhla nie je v  definovaná, lebo pre
definovaná, lebo pre  by bol menovateľ (kosínus uhla) rovný 0 -preto graf vyzerá tak ako vyzerá ("prerušený")...
by bol menovateľ (kosínus uhla) rovný 0 -preto graf vyzerá tak ako vyzerá ("prerušený")...
Myslím, že uvedomiť si, kde sú hodnoty v ä č š i e od nejakých daných sa dá pri uvážení toho, že tangens uhla je r a s t ú c a funkcia...
Offline

![kopírovat do textarea $y=\sqrt[4]{\ln\tan x}$](/mathtex/ae/ae968d940fa1a08b9953a4d312a16229.gif)