Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 10. 2011 15:45
Potřebuju pomoc
Ahoj,
dlouho jsem do matiky nic nedělal a teď nadešel čas, kdy musím. Ikdyž mám střední školu již za sebou, píši to sem. Budu rád za pomoc s postupem u jakéhokoli příkladu. Knížky mi moc nepomohly.
1) Určete periodu funkce a dokažte, jedná-li se o lichou funkci
f(x)=log(cosx)
2) 15.3^x+2+3^x=112
3) Určete definiční obor
\sqrtsix+1/sinx-1
4) Řešte v R
1+cosx+cos2x=sinx+sin2x+sin3x
Offline
- (téma jako vyřešené označil(a) SpecialD)
#2 16. 10. 2011 15:54
- cyrano52

- Místo: Frýdek-Místek
- Příspěvky: 705
- Škola: VŠB-TUO Ekonomická fakulta
- Pozice: student
- Reputace: 29
Re: Potřebuju pomoc
u 2) logaritmovat: 16.3^x=110
log(16) + xlog(3) = log(110)
xlog(3) = log(110) - log(16)
x = (log(110)-log(16))/log(3)
x = 1,7548
Největší bohatství je vzdělání - R. Kiyosaki
Offline
#3 16. 10. 2011 16:13
- marnes

- Příspěvky: 11227
Re: Potřebuju pomoc
↑ SpecialD:
nebo
2) 15.3^x+2+3^x=112 /-2
15.3^x+3^x=110
16.3^x=110 /:16
3^x=110/16 a zlogaritmovat
xlog3=log(110/16)
x=log(110/16)/log3
výsledek stejný
Jo. A na začátku vás zdravím.
Offline
#5 16. 10. 2011 16:20
Offline
#6 16. 10. 2011 16:22
Offline
#7 16. 10. 2011 16:23
#8 16. 10. 2011 16:23
Re: Potřebuju pomoc
1) cos(x) má periodu 2pí, takže log(cos(x)) má periodu taky 2pí.
Dále, cos(x) je sudá fce a log(x) není ani sudá ani lichá, takže celá funkce log(cos(x)) lichá určitě být nemůže.
Jinak pro sudost/lichost funkcí platí pár pravidel:
Nevím, jestli se dá udělat podobná tabulka i pro složené funkce, tam to asi záleží na konkrétních případech, ale tahle funkce je zrovna sudá, protože je to logaritmus sudé funkce, takže do hodnoty toho logaritmovaného výrazu ti nalevo i napravo od osy y padají ta samá čísla.
Offline
#9 16. 10. 2011 16:31
Offline
#11 16. 10. 2011 17:06 Příspěvek uživatele Lucy96 byl skryt uživatelem Lucy96.
#13 16. 10. 2011 17:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Potřebuju pomoc
↑ SpecialD:
proč musíš? VŠ vzdělání není povinné.
Dodržuj, prosím, pravidla a také pokyny pro matematické zápisy a v tom smyslu si založ nové téma pro def. obor. Děkuji.
Zdravím v tématu :-)
Offline
#14 16. 10. 2011 17:32
Re: Potřebuju pomoc
↑ Pajitko:
Kde se vzala ta odmocnina ze šesti?
Jelena: Omlouvám se, příště se to nestane :-)
Offline
#15 16. 10. 2011 17:36
Re: Potřebuju pomoc
↑ SpecialD:
↑ Pajitko: má smysl pro humor a přeložil si "six" jako 6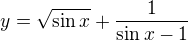
dvě podmínky: 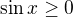
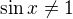
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#17 16. 10. 2011 17:46 — Editoval SpecialD (16. 10. 2011 17:49)
Re: Potřebuju pomoc
↑ SpecialD:
A co kdyby byl pod odmocninou třeba celý ten výraz u def. oboru, byl by výsledek stejný, že? Mám na mysli odmocninu a v ní zlomek. Sinx+1/sinx-1
Offline
#18 16. 10. 2011 18:16 — Editoval Pajitko (16. 10. 2011 18:19)
Re: Potřebuju pomoc
↑ zdenek1:
Smysl pro humor měl zrovna lepší věci na práci, jen jsem na chvilku zapomněl, v jaké žiju zemi :D ale je fajn, žes to ode mě bral jako záměr :-)
SpecialID napsal(a):
A co kdyby byl pod odmocninou třeba celý ten výraz u def. oboru, byl by výsledek stejný, že? Mám na mysli odmocninu a v ní zlomek. Sinx+1/sinx-1
Tak celý výraz nesmí být záporný, takže buď je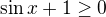 a zároveň
a zároveň 
nebo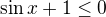 a zároveň
a zároveň 
ale myslím, že takové podmínky splňuje jen hodnota sinx=-1
Edit: jestli jsi teda myslel 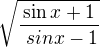
Offline
#19 16. 10. 2011 18:26
Re: Potřebuju pomoc
↑ Pajitko:
Ano, myslel jsem tento výraz. Takže výsledek je sinx se nesmí rovnat méně jedné?
Offline
#20 16. 10. 2011 18:39
Re: Potřebuju pomoc
↑ SpecialD:
Naopak, pro tenhle výraz musí být sinx=-1, ve všech ostatních případech bude nahoře kladné číslo a dole záporné, protože sinx má obor hodnot jen od -1 do 1, takže celý zlomek bude záporný. Jediná výjimka je právě sinx=-1, protože pak ti nahoře vyjde nula, tzn. celý zlomek bude nula.
Ale to už jsme se dostali od původního tématu dost daleko, hodně štěstí se studiem :-)
Offline

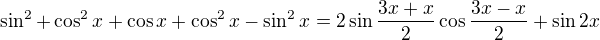
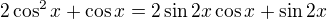
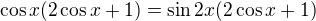

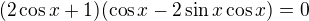
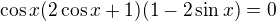
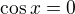 nebo
nebo  nebo
nebo 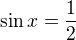
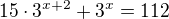 Takhle?
Takhle?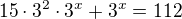
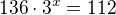
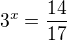
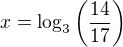
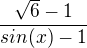
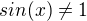 , takže
, takže 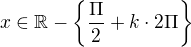 kde k je jakékoli celé číslo
kde k je jakékoli celé číslo