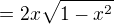Matematické Fórum

Hanis · 16. 10. 2011 17:17 — Editoval Hanis (16. 10. 2011 17:35)

Zadání:
$\int\sqrt{1-x^2}dx=$
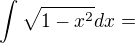
Zavedl jsem substituci
$x=sin t$
$dx=cost~dt$
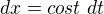
tedy
$=\int cos^2t ~dt=\int\frac{1+cos2t}{2}dt=\frac{t}{2}+\frac12\int cos2t~dt=$
Další substituce:
$2t=z$
$2dt=dz$
$=\frac{t}{2}+\frac14\int cosz~dz=\frac{t}{2}+\frac{sinz}{4}=$
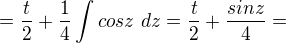
A teď nastává problém u zpětné substituce:
$=\frac{arcsinx}{2}+\frac{sin(2arcsinx)}{4}$

Neumím upravit výraz $sin(2arcsinx)$
Wolfram si s tím poradí, ale mně se to nedaří.
Mimochodem: v materiálech, s kterými pracuji, je naznačeno řešení skrzeva per partes $u^{\prime}=1$ a $v=\sqrt{1-x^2}$ , což mi taky nepomohlo.
Děkuji za rady.

EDIT: překlepy

jelena · 16. 10. 2011 17:42

↑ Hanis:

Zdravím,

takovou úlohu jsem "rozebírala" (za pomocí sbírky od Hlaváčka) - tu zítra pošlu po Honzovi :-) Jinak doporučovaná substituce nakonec dovede ke stejnému výsledku.

Teď ještě nakopíruji z Hlaváčka řešení i s arcsin (za chvilku umístím, ať nemusím vypisovat). Proč úloha není v sekci VŠ? :-)

zdenek1

↑ Hanis:
Odkaz

$\sin(2\arcsin x)=2\sin(\arcsin x)\cos(\arcsin x)=2x\sqrt{1-\sin^2(\arcsin x)}=$
$=2x\sqrt{1-x^2}$

Hanis · 16. 10. 2011 18:18

Děkuji Vám oběma, ↑ tato: úprava mě nenapadla a přitom je tak elegantní.
Úloha není v sekci VŠ, protože ten integrál není dostatečně složitý, problém byl nakonec s cyklometrickou funkcí :)
@ Jelena: Za všechny materiály děkuju, ještě bychom se mohli domluvit na sobotní setkání :-)

jelena · 16. 10. 2011 18:19

↑ zdenek1:

:-) děkuji, to je to, co jsem byla líná vypisovat (máš vlastního Hlaváčka? Já, bohužel, ne).

Tak sem ještě umístím kopie obrázků z Hlaváčka: úloha 784, úloha 602, pokračování

jelena · 16. 10. 2011 19:59

↑ Hanis:

také děkuji, plánování zatím neplánuji (nechávám to až na sobotní ráno :-), kolega Hanzy určitě pojede, to se naplánuje (pokud neomarodí, dohází nám zásoby teplého oblečení a obutí, všechno je postupně přesunuto do šatny MGO a nějak se nesune zpět :-). Omlouvám se za nereagování - zůstala jsem online, ale nebyla jsem v dosahu.

Matematické Fórum

#1 16. 10. 2011 17:17 — Editoval Hanis (16. 10. 2011 17:35)

neurčitý integrál

#2 16. 10. 2011 17:42

Re: neurčitý integrál

#3 16. 10. 2011 17:47 — Editoval zdenek1 (16. 10. 2011 17:54)

Re: neurčitý integrál

#4 16. 10. 2011 18:18

Re: neurčitý integrál

#5 16. 10. 2011 18:19

Re: neurčitý integrál

#6 16. 10. 2011 19:59

Re: neurčitý integrál

Zápatí