Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 17. 10. 2011 15:11
Re: Reciproké rovnice
↑ pepa999:
Ach, samozřejmě máte pravdu, ale jak tedy pokračovat? Omlouvám se, dnes mi to absolutně nemyslí.
Offline
#4 17. 10. 2011 15:18
Re: Reciproké rovnice
Já takové úlohy řeším tak, že nejdříve uhádnu jeden kořen a potom snížím stupeň mnohočlenu o jedna a potom se uvidí. Teď takové řešení asi akceptovat nebudeš, když už znáš správné výsledky, ale mám pocit, že u všech takových zadání, pokud je to pro střední školy, je vždycky jedno z řešení -3, -2, -1, 1, 2 nebo 3...
Offline
#6 17. 10. 2011 15:38 — Editoval CLieR (17. 10. 2011 15:49)
Re: Reciproké rovnice
My bereme (jsme zkoušeni) pouze z reciprokých rovnic V. a VI. stupně, kde dle Hornerova schématu dojdeme k recip. IV. stupně, jenže zde jsem se nějak zasekl. I když jsem si zvolil, že x^2 + 1/x^2 = y^2 - 2, tak sice vyjde kvadratická s pěknými kořeny (-1/3 a -15/6), ale při zpětné substituci to opět vychází špatně
EDIT: příklad za tímto, označen jako d) mi vyšel bez problému se stejným postupem, nejspíše jsem někde musel udělat numerickou chybu
Offline
#9 17. 10. 2011 16:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Reciproké rovnice
↑ CLieR:
jednou jsem skoro vyřešila kvadratickou rovnici, tak se opět pokusím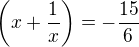

 už se podaří?
už se podaří?
Offline
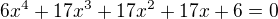



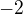 a
a 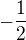
 a v 1. členu se objeví toto:
a v 1. členu se objeví toto: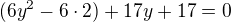
 . Děkuji.
. Děkuji.
 , podělit dvanácti a vyjde -1/3
, podělit dvanácti a vyjde -1/3
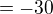 , podělit dvanácti a vyjde -15/6
, podělit dvanácti a vyjde -15/6