Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 19. 10. 2011 18:36 — Editoval vanok (19. 10. 2011 18:40)
Re: (Suma) Nalezení vzorce pro součet
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 19. 10. 2011 18:42 — Editoval vanok (19. 10. 2011 18:43)
Re: (Suma) Nalezení vzorce pro součet
↑ halogan:
Pockajme co nam napise ↑ Jirkaa:
Inac som pridal do mojej poznamky↑ vanok: aj formulu
TAK cakam
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 19. 10. 2011 18:56 — Editoval vanok (19. 10. 2011 18:57)
Re: (Suma) Nalezení vzorce pro součet
↑ Jirkaa:,
Jedna metoda je
Vie sa ze to je polynom tretieho stupna
Tak je takejto formy:
tak teraz vypocitaj niekolko hodnot 
Najpraktickejsie je to pre k= 1, 2, 3, a 4
A dosad to do 
To ti da linearny system co musis vyriesit... to dosadis do  a mas tvoj vzorecek
a mas tvoj vzorecek
A ak chces byt kompletny overis ho napr indukciou
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 19. 10. 2011 19:05
Re: (Suma) Nalezení vzorce pro součet
↑ vanok:
Co tím myslís "Vie sa ze to je polynom tretieho stupna"? Pokud bych neznal vzorec  , odkud vim, ze je to polynom tretiho stupne?
, odkud vim, ze je to polynom tretiho stupne?
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 19. 10. 2011 19:09 — Editoval vanok (19. 10. 2011 19:10)
Re: (Suma) Nalezení vzorce pro součet
↑ Pavel:
Povedzme ze je to nasa hypotheza.
A preto som pripisal ze <<A ak chces byt kompletny overis ho napr indukciou>> alebo inac
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 19. 10. 2011 21:51
Re: (Suma) Nalezení vzorce pro součet
↑ Pavel:
Nadhera
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 19. 10. 2011 22:39
Re: (Suma) Nalezení vzorce pro součet
↑ vanok:
Zdravím. Viete aj dokázať, že je to polynóm tretieho stupňa respektíve...Viete dokázať toto ?
Nech  . Explicitné vyjadrenie súčtu
. Explicitné vyjadrenie súčtu  -tých mocnín prvých
-tých mocnín prvých  prirodzených čísel je polynóm
prirodzených čísel je polynóm  . stupňa.
. stupňa.
1^6 - 2^6 + 3^6 = 666
Offline
#13 19. 10. 2011 22:56
Re: (Suma) Nalezení vzorce pro součet
↑ BakyX:
No prve co my prichadza na um je generalizovat Pavlovu metodu, co je ozaj jednoduche.
A to ti da mas priamo dokaz .
Pockaj minutu, pridam tu este jednu pristupnu metodu za niekolko minut.
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 19. 10. 2011 23:15
Re: (Suma) Nalezení vzorce pro součet
↑ BakyX:
ta ina metoda je bazovana na vypocte integralov
najprv mozes dokazat ze 
Ak toto aplikujes na i=1 az n a vsetky taketo relacie zratas dostanes
 a ak predpokladas ze toto formula plati pre 1 az n ( tu je indukcia) dostanes vysledok.
a ak predpokladas ze toto formula plati pre 1 az n ( tu je indukcia) dostanes vysledok.
Metoda co som dal pre Jirkaa je dokaz co sa tiez da generalizovat.; a da odpoved na tvoju otazku
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 20. 10. 2011 12:21
Re: (Suma) Nalezení vzorce pro součet
Mala poznamka( z mojich archivov): Uz velmi davno som sa este stretol z tymto zaujimavym vysledkom
kde 
 su Bernoulli-ho polynomy a
su Bernoulli-ho polynomy a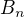 Bernoulli-ho cisla
Bernoulli-ho cisla
Dokaz sa najde v kazdej dobre knihe kombinatoriky
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 20. 10. 2011 12:46
Re: (Suma) Nalezení vzorce pro součet
↑ Jirkaa:
Už se to tady jednou někde řešilo (teď ovšem nemůžu najít kde)
Tak tedy odvození např. takto:
Offline
#17 20. 10. 2011 14:38
Re: (Suma) Nalezení vzorce pro součet
↑ Honzc:
Já také jsem to tu už řešil, ale marně to hledám ... :-(
Vezměme posloupnost, jejímž n-tým členem je  , kde
, kde  je přirozené číslo. Potom prvou diferencí této posloupnosti bude
je přirozené číslo. Potom prvou diferencí této posloupnosti bude
posloupnost  , kde
, kde
 ,
,
což je polynom stupně  (v proměnné
(v proměnné  ) , jak se snadno přesvědčíme rozvojem
) , jak se snadno přesvědčíme rozvojem  podle binomické věty. Odtud vyplývá:
podle binomické věty. Odtud vyplývá:
Je-li 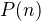 polynom stupně
polynom stupně  , potom
, potom  je polynom stupně k-1 .
je polynom stupně k-1 .
Zpětnou úvahou dostáváme tip:
Je-li dán polynom  stupně
stupně  a hledáme-li funkci
a hledáme-li funkci 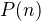 takovou, aby
takovou, aby  , pak hledejme
, pak hledejme 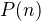 ve tvaru
ve tvaru
polynomu stupně  .
.
Spaciálně tedy:
Jestliže  , potom
, potom  , což je polynom stupně 2. Takže podle
, což je polynom stupně 2. Takže podle
předchozích úvah je rozumné očekávat  ve tvaru polynomu stupně 3.
ve tvaru polynomu stupně 3.
Offline
#19 20. 10. 2011 15:17
Re: (Suma) Nalezení vzorce pro součet
↑ Rumburak:
co pises propomina Newton-ove konecne differencie
Je to znama metoda co ti pomoze napisat hocijaky polynom v base typu 
Jej jeduina vyhoda je prist k polynomu z minomov vypoctov
z minomov vypoctov
Hladajte to v knihach z numerickej analyzy alebo o konecnych differenciach
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#20 20. 10. 2011 16:09
Re: (Suma) Nalezení vzorce pro součet
V příspěvku #10 v tématu
http://forum.matweb.cz/viewtopic.php?id=11047
ukazuji, jak je možné najít součet bez předpokladu o tom, že výsledek bude ve tvaru polynomu.
Offline
#21 20. 10. 2011 17:13 — Editoval vanok (07. 04. 2012 11:22)
Re: (Suma) Nalezení vzorce pro součet
Este jedna illustracna poznamka( nebudem tu rozvadzat celu teoriu)
Methoda co som ako poslednu citoval nas vedie k tabulke "konecnych diferencii"
1; 8; 27; 64;
7; 19; 37
12; 18
6
0; od piateho riadku budu len nuly ....
co nam LAHKO da

TATO methoda by mala byt v kazdej prednaske zakladov numerickej matematiky.
Historicky sa zda ze sa taketo metody uz pouzivali v Starej Cine.
Srdecne VANOK
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline



![kopírovat do textarea $
\sum_{i=1}^{n+1} i^3&=\sum_{i=1}^{n+1} \bigl(1+(i-1)\bigr)^3\\
\sum_{i=1}^{n+1} i^3&=\sum_{i=1}^{n+1} \bigl(1+3(i-1)+3(i-1)^2+(i-1)^3\bigr)\\
\sum_{i=1}^{n+1} i^3&=\sum_{i=1}^{n+1} 1+3\sum_{i=1}^{n+1}(i-1)+3\sum_{i=1}^{n+1}(i-1)^2+\sum_{i=1}^{n+1}(i-1)^3\\
\sum_{i=1}^{n+1} i^3&=\sum_{i=1}^{n+1} 1+3\sum_{i=0}^n i+3\sum_{i=0}^n i^2+\sum_{i=0}^n i^3\\
\sum_{i=1}^{n+1} i^3-\sum_{i=0}^n i^3&=n+1+3\cdot\frac n2\,(n+1)+3\sum_{i=1}^n i^2\\
(n+1)^3&=(n+1)+\frac 32\,n(n+1)+3\sum_{i=1}^n i^2\\
3\sum_{i=1}^n i^2&=\frac 12\,(n+1)[2(n+1)^2-2-3n]\\
\sum_{i=1}^n i^2&=\frac 16\,n(n+1)(2n+1).
$](/mathtex/78/780367c4b5e89cedb49d039c04522694.gif)

