Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 10. 2011 21:00 — Editoval Mihulik (18. 10. 2011 21:01)
Induktivně zadaná funkce
Ahoj,
zadání příkladu zní:
Pro funkci  a
a 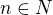 definujeme induktivně funkci
definujeme induktivně funkci 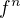 takto:
takto: 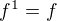 a
a  .
.
Nechť X je konečná množina a 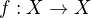 je funkce. Dokažte, že existují dvě různá přirozená čísla r, s taková, že
je funkce. Dokažte, že existují dvě různá přirozená čísla r, s taková, že  .
.
Intuitivně si nějak umím představit, že to platí (definuji si nějakou konečnou množinu, určim si vztahy mezi prvky této množiny a pak je vidět, že z jednoho prvku na jiný se dokážu dostat ve dvou různých počkech kroků), ale jak formálně do důkazu vůbec netuším.
Mohl by mi prosím někdo poradit, jak vůbec začít?
Děkuji:)
Offline
#2 18. 10. 2011 21:28 — Editoval vanok (18. 10. 2011 22:00)
Re: Induktivně zadaná funkce
↑ Mihulik:
Je to lahko vidiet,
X je konecna mnozina , oznacim k pocet jej prvkov.
Aby sa to lahsie vyjadrilo budem pracovat na mnozine 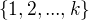
Je jasne ze obraz 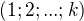 je
je 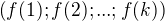 a na to mame
a na to mame  moznosti
moznosti
preto najneskor po 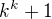 krokoch musi byt opakovanie.
krokoch musi byt opakovanie.
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 19. 10. 2011 20:41
Re: Induktivně zadaná funkce
vanok napsal(a):
↑ Mihulik:
X je konecna mnozina , oznacim k pocet jej prvkov.
Aby sa to lahsie vyjadrilo budem pracovat na mnozine
Je jasne ze obrazje
a na to mame
moznosti
Děkuji za radu. Do této chvíle to plně chápu, ovšem toto
vanok napsal(a):
preto najneskor po
krokoch musi byt opakovanie.
už nějak nemůžu pochopit:-/ Nevím, jak z toho plyne, že takové r a s existují... Mohl bys mi to prosím ještě trošku zkusit rozepsat?
děkuji:)
Offline
#4 20. 10. 2011 09:43 — Editoval Rumburak (20. 10. 2011 13:45)
Re: Induktivně zadaná funkce
↑ Mihulik:
Nechť  je pevně daná
je pevně daná  -prvková množina (kde
-prvková množina (kde  je přirozené číslo) a
je přirozené číslo) a  je množina všech funkcí tvaru
je množina všech funkcí tvaru 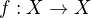 .
.
Víme, že množina  má
má 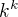 prvků (s hlediska středoškolské kombinatoriky je
prvků (s hlediska středoškolské kombinatoriky je  množina všech variací
množina všech variací  -té třídy z
-té třídy z  prvků s opakováním).
prvků s opakováním).
Tedy množina  má pouze konečně mnoho prvků .
má pouze konečně mnoho prvků .
Zvolme pevně  a sestrojme funkční posloupnost
a sestrojme funkční posloupnost  podle dané rekurentní formule. Pro každý její člen je
podle dané rekurentní formule. Pro každý její člen je 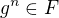 ,
,
tudíž množina  jakožto část konečené množiny
jakožto část konečené množiny  je rovněž konečná. Takže posloupnost
je rovněž konečná. Takže posloupnost  nemůže být prostá,
nemůže být prostá,
protože v takovém případě by množna 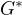 musela být nekonečná.
musela být nekonečná.
Poznámka: Způsob, jak byla sestrojena posloupnost G, aby jejími členy byly pouze prvky množiny F, nebyl vůbec podstatný. Z předchozích úvah je
jistě zřejmé, že žádná taková posloupnost by nemohla být prostá.
Offline
#5 20. 10. 2011 10:13 — Editoval vanok (20. 10. 2011 19:42)
Re: Induktivně zadaná funkce
↑ Mihulik:
Co sa tyka Dirichlevovho principu, ktory ma po anglicky nadherne meno <<Pigeonhole principle>>
je ozaj nutne ho dobre pochopit, lebo moze zjednodusit mnoho dokazov a nemysli si ze je to folklor co nema miesto v matematike
Ked pocitas 1/7, preco od urciteho miesta sa zacnu opakovat podiely?
Uz aj v beznom zivote ak ma sadnut 11 ludi na 10 stoliciek; co prve ti napadne?
A na ceskej wikipedii, co som ti dal vysie si mohol citat ( a skus to tento weekend sa spytat tvojich spolocnikov pri nedelnom obede) najdes <<Ačkoliv zní princip jednoduše, může být použit k dokázání na první pohled nečekaných výsledků. Můžeme např. dokázat, že v Praze žijí dva lidé, kteří mají přesně stejný počet vlasů. Uvážíme-li, že počet vlasů jednoho člověka nikdy nepřesahuje 1 000 000 a v Praze žije více než 1 000 000 lidí – pak musí být alespoň dva, kteří mají stejný počet vlasů.>>
Mozno ti niekto bude namietat ze na dokaz tohto principu treba AXIOMU VYBERU, ale v beznej matematike je prijata ...
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 20. 10. 2011 19:22
- check_drummer

- Příspěvky: 4628
- Reputace: 99
Re: Induktivně zadaná funkce
vanok napsal(a):
↑ Mihulik:
Mozno ti niekto bude namietat ze na dokaz tohto principu treba AXIOMU VYBERU, ale v beznej matematike je prijata ...
Myslím, že pokud se pohybujeme v množinách s konečnou mohutností, tak axiom výběru není potřeba.
"Máte úhel beta." "No to nemám."
Offline
#7 20. 10. 2011 19:41
Re: Induktivně zadaná funkce
↑ check_drummer:
To mas pravdu, ale som myslel na vsetki mozne generalizacie principu. Mal som skor explicitne napisat <<Mozno ti niekto bude namietat ze na dokaz tohto principu treba AXIOMU VYBERU, ale v beznej matematike je prijata ...alebo aj niekedy nepotrebna>>
Ale vsetci uzuvatelia mozu tento Dirchlet-ov princip pouzivat bez problemu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 21. 10. 2011 09:53
Re: Induktivně zadaná funkce
Děkuji vám všem. Teď už je mi to, po chvíli zamyšlení, jasné.:)
Dirchletův princip je intuitivně jasný, ale že ho lze formulovat i formálněji, jsem nevěděl - pořádně si to prostuduji.
Ještě jednou děkuji.:)
Offline
