Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 10. 2011 16:16
- tigerhell22
- Příspěvky: 63
- Reputace: 0
Definiční obor
zdravim,
1) ma daný takový to definiční obor 1-9x^(2)-9y^(2)>=0 a mam ho nakreslit, vim že to má být kružnice, konkretně její vnitřní část... ale jak poznam kde bude kružnice protinat osu x a y, v jakych číselných bodech ?
2) mam zrčit definiční obor f(x,y)=tg(x+2y) .. vyjde to takhle... y se nerovná (2k+1)*(pi/4) - (1/2)x ... mohl by mi to někdo prosím objasnit jak se k tomu přišlo ...
předem děkuji moc za odpověd
Offline
- (téma jako vyřešené označil(a) tigerhell22)
#3 24. 10. 2011 16:43
- tigerhell22
- Příspěvky: 63
- Reputace: 0
Re: Definiční obor
↑ halogan:
to jsem pochopil, ze se to dá takhle přepsat... ale už jsem zapoměl ty průsečíky... nevíš jak se to teda dělá ?
Offline
#4 24. 10. 2011 16:56
Re: Definiční obor
↑ tigerhell22:
Na osi x leža iba práve také body, ktorých súradnica y je 0.
Na osi y ležia iba práve také body, že icj súradnica x je 0.
Offline

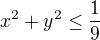
 . A jak se zjišťují průsečíky osami? Co platí vždy pro jednu ze souřadnic takového bodu?
. A jak se zjišťují průsečíky osami? Co platí vždy pro jednu ze souřadnic takového bodu?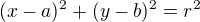 ,
,