Matematické Fórum

aralk09 · 04. 11. 2011 21:16 — Editoval jelena (09. 11. 2011 08:00)

ahoj, potřebovala bych poradit ještě s tímto polynomem $x^{4}+x^{2}+3$
Psala jsem sem myslím ve úterý, taky o pomoc polynomy..zkoušela jsem bin. rci, ale tam vychází odmocniny s kompl. čísla a aji pomocí vzorců (a-b).(a+b), ale tam jsem se zasekla a nevěděla jak dál...díky za radu ;)

************** kompletní řešení od kolegy Vanok (děkuji) *******************

Je jasne ze tvoj polynom sa faktorizuje na dva polynomy 2°.
Jedna metoda je najst vsetki jeho komplexne korene a potom vytvorit dva realne polynomy 2° pomocou tych korenov.

No ja by som tu pouzil skor, toto:
Ak $x^{4}+x^{2}+3$ sa faktorisuje ako sucin dvoch polynomov 2°, tak
$x^{4}+x^{2}+3= (X^2 + aX + b)(X^2 +cX+ d)$
pre a, b, c, d realne cisla.

A teraz sama pokracuj

vynasob tie dva polynomy a porovnaj koefiecienty

To ti da 4 rovnice, a jedno z rieseni bude to co hladas... necakaj ze budes mat celociselne riesenie.

ODPOVED:
$a=-c= \sqrt{2\sqrt3 -1}$
$b=d= \sqrt3$

Co nam da
$x^{4}+x^{2}+3= (x^2 + x\sqrt{2\sqrt3 -1} + \sqrt3 )(x^2 -x\sqrt{2\sqrt3 -1}+ \sqrt3 )$

A aby si videla ze moj vysledok je ok, mas tu aj skusku:
$(x^2 + x\sqrt{2\sqrt3 -1} +\sqrt3)(x^2 -x\sqrt{2\sqrt3 -1}+ \sqrt3 )= $ x^2 +\sqrt3 $^2 -$ x\sqrt{2\sqrt3 -1}$^2=$
$(x^4 +2x^2 \sqrt3 +3)-x^2(2\sqrt3 -1)= x^{4}+x^{2}+3$

Jedinu radu co ti mozem este dat, treba byt metodicky v takychto vypoctoch.

mikl3 · 04. 11. 2011 21:33

↑ aralk09: nevím přesně co potřebuješ, ale když zavedeš $S: y=x^2$ pomůže?

aralk09 · 04. 11. 2011 22:03

↑ mikl3:
Ty jo já jsem uplně zapomněla zadání, pardon...Mám to rozložit na součin ireducibilních polynomů. A substituci jsem také už zkoušela a pořád nic :/

((:-)) · 04. 11. 2011 22:33 — Editoval ((:-)) (04. 11. 2011 22:34)

↑ aralk09:

Ahoj.

Použila som finty kolegov z Tvojho predchádzajúceho príspevku.

$x^4+ x^2 + 3 = (x^4+4x^2 + 4)-(1+3x^2) = \cdots$

aralk09 · 05. 11. 2011 15:59

↑ ((:-)):
Takže pochopila jsem to správně, že když budu upravovat nějaký takový polynom tak tam přičtu a odečtu nějaký člen, abych mohla doplnit na čtvrec a pak už to upravit podle vzorečku $a^{2}-b^{2}$ ? Je to tak?

jelena · 05. 11. 2011 23:08

↑ aralk09:

Zdravím, postupů na úpravu může být více (např. zde bavím publikum) - cíl je sestavit součin dál nerozložitelných. Ale Tvé zadání se mi nepodařilo rozložit, snad někdo z kolegů potvrdí nebo vyvrátí. Děkuji.

((:-)) · 06. 11. 2011 00:10

↑ jelena:

Ahoj.

Odmocniny v rozklade nesmú byť?

aralk09 · 06. 11. 2011 11:34

↑ jelena:
Mně to vyšlo $(x^{2}+2-\sqrt{1+3x^{2}}).(x^{2}+2+\sqrt{1+3x^{2}})$ a když se to roznásobí, tak to vychází, tak nevím jestli ty odmocniny tam můžou být nebo ne, ale přece jenom jsou to také čísla...

jelena · 06. 11. 2011 12:31

↑ aralk09:

podle mne v rozkladu polynomu nemůže být (1+3x^2)^(1/2) - porovnej, prosím, s definici. Děkuji.

aralk09 · 06. 11. 2011 14:44

↑ jelena:
No s definicí polynomu to nesedí, exponenty mají být jen celočíselné. Tak nevím, ale zase kdyby se to nedalo rozložit, tak bych to neměla za úkol rozložit na součin...jedině snad kdyby to byl chyták...

vanok · 06. 11. 2011 15:19 — Editoval vanok (06. 11. 2011 15:25)

Ahoj ↑ aralk09:,

Mas uplne pravdu.

Je jasne ze tvoj polynom sa faktorizuje na dva polynomy 2°.
Jedna metoda je najst vsetki jeho komplexne korene a potom vytvorit dva realne polynomy 2° pomocou tych korenov.

No ja by som tu pouzil skor, toto:
Ak $x^{4}+x^{2}+3$ sa faktorisuje ako sucin dvoch polynomov 2°, tak
$x^{4}+x^{2}+3= (X^2 + aX + b)(X^2 +cX+ d)$
pre a, b, c, d realne cisla.

A teraz sama pokracuj

vynasob tie dva polynomy a porovnaj koefiecienty

To ti da 4 rovnice, a jedno z rieseni bude to co hladas... necakaj ze budes mat celociselne riesenie.

Cakam na tvoju odpoved pre kontrolu.

Srdecne Vanok

The respect, the politeness are essential qualities.
Do not judge the other one.

aralk09 · 06. 11. 2011 22:47

↑ vanok:
Tak jsem to spočítala a vyšla mi nakonec soustava dvou rovnic (jedna lineární, druhá kvadratická)o dvou neznámých(s céčkem a déčkem), tak jsem to nějak spočítala dál, ale vyšlel mi záporný diskriminant ,a co s tím dál, to opravdu netuším..:/

vanok · 06. 11. 2011 23:16 — Editoval vanok (06. 11. 2011 23:16)

↑ aralk09:
dam ti odpoved, ale si sa zmylila niekde.
A naviac si videla co som napisal, sucin dvoch polynomov 2°.

ODPOVED:
$a=-c= \sqrt{2\sqrt3 -1}$
$b=d= \sqrt3$

Co nam da
$x^{4}+x^{2}+3= (x^2 + x\sqrt{2\sqrt3 -1} + \sqrt3 )(x^2 -x\sqrt{2\sqrt3 -1}+ \sqrt3 )$

A aby si videla ze moj vysledok je ok, mas tu aj skusku:
$(x^2 + x\sqrt{2\sqrt3 -1} +\sqrt3)(x^2 -x\sqrt{2\sqrt3 -1}+ \sqrt3 )= $ x^2 +\sqrt3 $^2 -$ x\sqrt{2\sqrt3 -1}$^2=$
$(x^4 +2x^2 \sqrt3 +3)-x^2(2\sqrt3 -1)= x^{4}+x^{2}+3$

Jedinu radu co ti mozem este dat, treba byt metodicky v takychto vypoctoch.

Srdecne Vanok

The respect, the politeness are essential qualities.
Do not judge the other one.

aralk09 · 07. 11. 2011 21:14

↑ vanok:
Je to tato soustava rovnic:
c+a=0
d+ac+b=1
ad+bc=0
bd=3, že jo?
Vůbec nevím, kde dělám chybu, počítám to už 2 dny a pořád mi to vychází stejně...

vanok · 07. 11. 2011 22:29 — Editoval vanok (07. 11. 2011 22:43)

Ahoj ↑ aralk09:,

No vsak ak to robis po poriadku je to lahke.
Prva rovnica ti da c=-a
Tretia sa da napisat a(d-b)=0, a nemoze byt 0, PRECO?
Tak mame d=b
Posledna nam da b=d= +alebo - 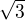$\sqrt3$

Pouzi teraz druhy co ti da $a^2=2b-1$
Akoze $a^2>0$ tak aj $b$ musi byt tiez >0, co znamena ze....

Mas ozaj stastie ze som priliz trpezlivy

Srdecne Vanok

The respect, the politeness are essential qualities.
Do not judge the other one.

Matematické Fórum

#1 04. 11. 2011 21:16 — Editoval jelena (09. 11. 2011 08:00)

polynom

#2 04. 11. 2011 21:33

Re: polynom

#3 04. 11. 2011 22:03

Re: polynom

#4 04. 11. 2011 22:33 — Editoval ((:-)) (04. 11. 2011 22:34)

Re: polynom

#5 05. 11. 2011 15:59

Re: polynom

#6 05. 11. 2011 23:08

Re: polynom

#7 06. 11. 2011 00:10

Re: polynom

#8 06. 11. 2011 11:34

Re: polynom

#9 06. 11. 2011 12:31

Re: polynom

#10 06. 11. 2011 14:44

Re: polynom

#11 06. 11. 2011 15:19 — Editoval vanok (06. 11. 2011 15:25)

Re: polynom

#12 06. 11. 2011 22:47

Re: polynom

#13 06. 11. 2011 23:16 — Editoval vanok (06. 11. 2011 23:16)

Re: polynom

#14 07. 11. 2011 21:14

Re: polynom

#15 07. 11. 2011 22:29 — Editoval vanok (07. 11. 2011 22:43)

Re: polynom

Zápatí