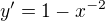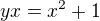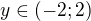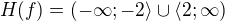Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Pomoc - vyšetření průběhu funkce a graf. (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 11. 2011 19:34 — Editoval jelena (10. 11. 2011 20:10)
- Shadowman23

- Zelenáč
- Příspěvky: 11
- Reputace: 0
Pomoc - vyšetření průběhu funkce a graf.
Zdravím všechny,studuji VS při zaměstnání, jsem ze školy cca 12 let. Matika je docela hard, máme příklady k počítání doma ale nějak se nechytám. Prosím o pomoc.
př. 1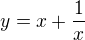
máme určit def.obor,sudost,lichost,periodičnost,intervaly:spojitosti a body nespojitosti,průsečíky grafu funkce s osami,intervaly kde je funkce:kladná,záporná,rostoucí,klesající,extrémy, intervaly kde je funkce konvexní,konkávní, inflexní body, asymptoty,limity funkce v krajních bodech definičního oboru a v bodech nespojitosti.
Procházím si skripta a dané příklady. Prosím o vzorový výpočet, popř. s komentářem. Jsem trochu v koncích, 15 let mimo školu je dost...
Předem Děkuji za Pomoc.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 10. 11. 2011 20:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc - vyšetření průběhu funkce a graf.
Zdravím,
vyšetřování 2 průběhů v jednom tématu bude velmi nepřehledné (i jeden je moc), proto jsem jedno zadání skryla do hide). Zde je místně oblíbený algoritmus, který je třeba krokově plnit - to bude "dělat co". V průběhu pravděpodobně budou vznikat momenty, kdy bude třeba vyřešit rovnici, nerovnici, derivovat apod. - to bude "dělat jak".
Pro vyřešení/kontrolu jednotlivých momentů je vhodné použit nástroje úvodního tématu sekce VŠ, doporučuji MAW, případně postupně vkládat sem problémové výpočty.
Zdar přeji.
Offline
#4 10. 11. 2011 20:20
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc - vyšetření průběhu funkce a graf.
↑ Alivendes:
já si nikdy nedělám starosti, já ji přidělávám jiným.
Nech kolegu, ať se trochu obeznámí s algoritmem - ze setkání, co jsi inicioval, vznikl takový úkol, ale nikde není psáno, že by průběhů s online podporou nemohlo vzniknout více. Tak se také můžeš realizovat, děkuji :-)
Offline
#5 10. 11. 2011 21:12 — Editoval Alivendes (13. 11. 2011 10:35)
Re: Pomoc - vyšetření průběhu funkce a graf.
Dobrý den, pokusím se trochu pomoct, spočítám první příklad, ten druhý snad zvládnete sám.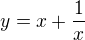

Definiční obor je množina všech přípustných x, můžeme dosadit cokoliv kromě nuly.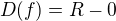
Obor hodnot dole popisuje kolega:
Periodická být nemůže, definiční obor jsou reálná čísla kromě nuly, tím pádem: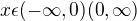
Funkce je lichá, protože platí:
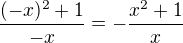
Funkce neprotíná ani osu x, ani osu y, ale platí že: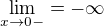
 Grafem je ,,hyperbola,,
Grafem je ,,hyperbola,,
Funkce je kladná pro  a záporná pro
a záporná pro 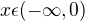
Nyní se můžeme vrhnout na extrémy, spočítáme první derivaci:


Nyný, když máme spočítanou derivaci, můžeme hledat stacionární body, případně extrémy. Víme, že v takovém bodě je derivace funkce nulová: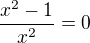
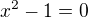
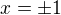
!!!!!!!!!-Máme funkci rozdělenou do dvou intervalů spojistosti, budeme hledat extrém pro každé rameno hyperboly.
Právě jsme vypočítali stacionární body funkce, ve kterých by mohl být extrém. To zjistíme pomocí druhé derivace, která pokud je kladná, v bodě je lokální minumum, naopak, pokud je záporná, v bodě je lokální maximum, popřípadě pokud je nulová, není to ani maximum ani minimum:
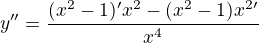
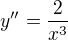
Teď máme spočítanou druhou derivaci, dosadíme body:
a)
Druhá derivace je v tomto bodě záporná, tím pádem platí pro :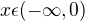 - funkce má v bodě -1 lokální maximum
- funkce má v bodě -1 lokální maximum
b)
Druhá derivace je v tomto bodě kladná, funkce zde má lokální minimum pro 
Pro jistotu si ukážeme graf, ze kterého by to mělo jít hezky vidět:
Konvexnost a konkávnost budeme opět vyšetřovat pro každou větev hyperboly zvlášť. V místech kde je druhá derivace kladná je funkce konvexní, naopak tam, kde je záporná, je funkce konkávní. Tohle nebude těžké. (Je to popřípadě vidět z grafu, který ale nebyl podmínkou)
a)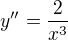
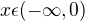
Záporné číslo umocněné natřetí bude vždy záporné, kladných hodnot tedy druhá derivace nabývat nebude, můžeme tedy říct, že funkce je na tomhle intervalu konkávní.
b)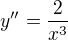

Naopak zde bude druhá derivace vždy kladná, funkce je tedy na tomhle intervalu konvexní.
Inflexní bod je takový, kde se funkce mění z konvexní na konkávní nebo naopak. V takovém bodě je druhá derivace nulová.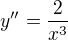
Tohle se ovšem nule nikdy rovnat nebude. Inflexní body tedy nejsou.( I tohle je možno vidět z grafu)
Nakonec spočítáme rovnice asymptot, to jsou přímky, které se s hyperbolou setkají v nekonečnu - lepší dle definice .
Je vidět, že jednou asymptotou bude osa y, druhou pak přímka dělící kvadrant na dvě části:
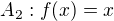
Doufám, že jsem na nic nezapomněl, přeji hezký zbytek večera.
P.S. Jinak jak říkala ↑ jelena:, je dobré nastudovat nějaké texty zkusit spočítat druhý příklad, kdyby jsi měl problém, můžeš s tím přijít sem. Velmi nápomocné je také Tohle
Jelena: doplnila jsem 2 červené poznámky, zbytek méně podstatných doporučení je v příspěvku 10 v hide
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#6 10. 11. 2011 21:40
Re: Pomoc - vyšetření průběhu funkce a graf.
↑ Alivendes:
Zdravim, krasne si protirecis :)
Obor hodnot je množina všech přípustných y, tedy hodnot, kterých funkce může nabývat, je vidět, že funkce může nabývat jakékoli hodnoty:
Funkce neprotíná ani osu x, ani osu y
Jinak, myslim, ze je trochu zbrkle ze dvou limit jdoucich k nule prohlasit, ze funkce je hyperbolou, vypada to, jako bychom resili priklad a opirali se u toho na vysledek, ke kteremu se mame dopracovat.
Jeste bych podotkl, ze stacionarni body a inflexni body se mohou vyskytovat i tam, kde pripadna derivace neni definovana, to je potreba take osetrit.
Co se tyce asymptot, tak bych nepouzival frazi "je videt", ale radsi rozdelil asymptoty na bez smernice a se smernici a spocital je klasicky a ne pomoci grafu.
Doufam, ze nejsem moc za hnidopicha.
Pekny vecer,
Phate.
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#8 10. 11. 2011 21:48
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc - vyšetření průběhu funkce a graf.
↑ Alivendes:
děkuji, je to moc hezké :-) až na online nástroje - kde jsou? nějaké drobnosti jsem vypsala do textu, omlouvám se za červenou, jen abych to viděla.
Ať se vede i nadále.
Offline
#9 10. 11. 2011 21:49
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc - vyšetření průběhu funkce a graf.
↑ Alivendes:
:-) kde jsou mé poznámky? Děkuji.
Offline
#10 10. 11. 2011 21:52
#13 10. 11. 2011 21:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc - vyšetření průběhu funkce a graf.
↑ Alivendes:
:-) teď jsou v příspěvku 10 v hide, ale to podstatné již opravujete - obor hodnot, jinak to jsou jen usnadňující kroky.
Offline
#14 11. 11. 2011 00:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoc - vyšetření průběhu funkce a graf.
↑ Alivendes:
bohužel, ale obor hodnot jsi neopravil ani pro dalším upozornění kolegy ↑ Phate:, doplnila jsem poznámku do Tvého textu (také k výpočtu asymptot).
Neber to, prosím, tak, že do Tvého jinak podrobně a náročného na čas a na úpravu příspěvku jen vrtáme, ale kolega ↑ Shadowman23: píše, že i tak se potyká s nastudováním látky, potom bude dobré, když také sám projde doporučovaný algoritmus z mathonline a ještě se poptá na nejasné momenty.
Mějte se pěkně, děkuji.
Offline
#15 11. 11. 2011 01:07 — Editoval Phate (11. 11. 2011 07:17)
Re: Pomoc - vyšetření průběhu funkce a graf.
Kdyztak ten obor hodnot se da resit takto:
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#16 11. 11. 2011 06:52 — Editoval ((:-)) (11. 11. 2011 13:40)
#19 12. 11. 2011 17:38
- Shadowman23

- Zelenáč
- Příspěvky: 11
- Reputace: 0
Re: Pomoc - vyšetření průběhu funkce a graf.
měl bych prosbu, jak přesně jste počítal asimptoty??
Offline
#20 12. 11. 2011 21:30 — Editoval Alivendes (12. 11. 2011 21:51)
Re: Pomoc - vyšetření průběhu funkce a graf.
Asymptoty můžeme dále rozdělit na asymptoty se směrnící bez směrnice.
a) Asmyptota bez směrnice je přímka, která je kolmá na osu x, v našem případě je asymptotou osa y a to je vidět z grafu.
Jinak platí, že pokud je funkce, jejíž definiční obor: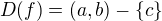
Dále pokud platí, že funkce má v tomto bodě c alespoň jednu jednostrannou nevlastní limitu, tak potom: Tahle přímka se jmenuje asymptotou bez směrnice.
Tahle přímka se jmenuje asymptotou bez směrnice.
V našem případě:
Také platí, že: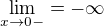

Tím pádem  je asymptotou bez směrnice naší funkce.
je asymptotou bez směrnice naší funkce.
b) Když chceme vypočítat asymptoty se směrnicí, je třeba si uvědomit, že asymptota je přímka, jejíž vzdálenost se limitně zmenšuje, až se s ní v nekonečnu protne. Musí platit:
Rovnice asymptoty: 
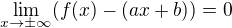
Můžeme psát, že: Čitatel bude vždy roven nule.
Čitatel bude vždy roven nule.
Tohle můžeme rozdělit do tří limit.
1) Výpočet koeficientu a :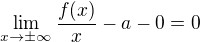
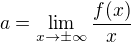
2) Výpočet koeficientu b :


Náš případ:
a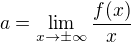

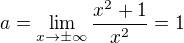
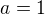
b

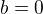
Naše asymptota se směrnicí: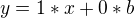
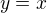
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#21 13. 11. 2011 11:41
- Shadowman23

- Zelenáč
- Příspěvky: 11
- Reputace: 0
Re: Pomoc - vyšetření průběhu funkce a graf.
↑ Alivendes:
Děkuji, je to o trochu jasnější. Další krok kupředu..
Offline
#22 24. 10. 2012 19:39 — Editoval Zuzka1994 (24. 10. 2012 19:45)
Re: Pomoc - vyšetření průběhu funkce a graf.
Dobrý den, ve škole probíráme průběh funkcí. Zkoušela jsem si vypočítat pár příkladů a narazila jsem na jeden u kterého si fakt nevím rady. Nejsem si jistá s sudostí,lichostí,periodičností... dále nevím jak určit: intervaly:spojitosti a body nespojitosti, intervaly kde je funkce:kladná,záporná,rostoucí,klesající,extrémy, intervaly kde je funkce konvexní,konkávní, inflexní body, asymptoty...
Děkuji moc za pomoc a radu!!:)
Fuknce: (x+8)/6*\sqrt[3]{x^{5} } (třetí odmocnina z x na 5)
Zatím jsem určila
D=R
Vypočítala jsem i první a druhou derivaci, limita.
První derivace: y´=4/9*x^{2/3}*(x+5)
x1=-5, x2=0
Druhá derivace: y´´= (20/27*(x+2))/x^{1/3}
x1=-2
limita: limx→∞ (x+8)/6*∛5=∞
limx→-∞ (x+8)/6*∛5=∞
Doufám, že to co jsem zatím určila je dobře.
Offline
#23 24. 10. 2012 19:59
Re: Pomoc - vyšetření průběhu funkce a graf.
↑ Zuzka1994:
toto je rok stará téma a naviac je označená ako vyriešená.
myslím, že tu sa ti nikto nebude snažiť odpovedať.
preto doporučujem založiť si vlastnú tému a na úvod sa zoznámiť aj s pravidlami, lebo dodržiavanie pravidiel zvyšuje šancu na odpoveď.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Pomoc - vyšetření průběhu funkce a graf. (TOTO TÉMA JE VYŘEŠENÉ)
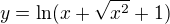


 :
: