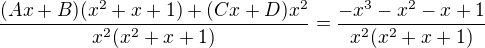Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 11. 2011 11:25
parcialni zlomky
potřebuji to rozlozit na parcialni zlomek a vubec nevim co s tim mam delat. (3x^5+2x^4+x^3-2x^2-x+1)/(x^4+x^3+x^2)
zkousela jsem to zkratit, vyslo mi (3x^3+2x^2-1)/(x^2+x+1)
pote jsem to vydelila a vyslo mi 3x-1*(2x/(x^2+x+1))
nevim jak to mam dale prevezt. Dekuji za pomoc
Offline
#2 12. 11. 2011 12:36
Re: parcialni zlomky
Ahoj,
je to čistě mechanická práce. Každej zlomek se rozkládá ve dvou krocích.
1) když je stupeň polynomu v čitateli větší nebo roven než ve jmenovateli, tak vydělit(postup se dá určitě najít třeba na seznamu). To ti dá buď výsledek, nebo v tomhle případě novej zlomek(zbytek toho dělení), kde stupeň polynomu nahoře je striktně menší než dole. Vyšlo mi 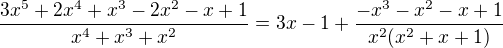 .
.
2) potom se na ten zbytek aplikuje metoda rozkladu, dá se najít třeba na http://tutorial.math.lamar.edu/Classes/ … tions.aspx
Rovnice k řešení tady bude 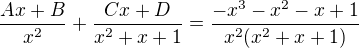
Offline
#5 12. 11. 2011 15:28 — Editoval ((:-)) (12. 11. 2011 15:41)
Re: parcialni zlomky
↑ Petra20: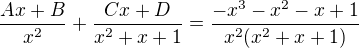
Tie zlomky na ľavej strane dáš na spoločný menovateľ, čitateľ roznásobíš a vytvoríš členy s rovnakou mocninou x.
Potom koeficienty s A,B,C,D porovnáš s čitateľom zlomku vpravo.
Pri x na tretiu je vpravo -1 - tak aj vľavo pri x na tretiu musí byť -1 ...
Dostaneš sústavu pre A,B,C,D a vyriešiš ju ...
Aj na fóre je viacero úloh na parciálne zlomky ...
Toto sa mi zdá veľmi prínosné ...
Offline