Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prázdninový integrál (TOTO TÉMA JE VYŘEŠENÉ)
#2 30. 07. 2008 13:29 — Editoval Jorica (30. 07. 2008 13:30)
Re: Prázdninový integrál
Pokud bych na to sla "silou", rozlozila bych jmenovatele 
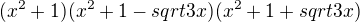
a pote postupovala pres rozklad na parcialni zlomky. Ale popravde se mi resit tu neprijemnou soustavu sesti rovnic o sesti neznamych "rucne" moc nechce. Takze doufam, ze nekdo na to pujde spis hlavou, nez silou :-)
Offline
#3 30. 07. 2008 13:38
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninový integrál

Vzhledem k tomu, že ten integrál nevychází moc hezky, tak to asi jinak než přes parciální zlomky nepůjde.
Offline
#4 30. 07. 2008 14:04
Re: Prázdninový integrál
↑ BrozekP:
Jo, protoze v tom rozkladu na parczlomky vyjdou jen koeficienty "bez x", povedou vsechny integraly (jeden primo a zbyvajici po doplneni na ctverec) na arctan, jak je uvedeno. Ale priznavam se dobrovolne, ze ten rozklad mi vypocitala technika, v tou vedru jsem nejaka lina ;-)
Offline
#5 30. 07. 2008 15:25 — Editoval BrozekP (30. 07. 2008 20:05)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninový integrál
↑ Pavel:
Měl jsem na mysli něco těžšího, racionální lomené funkce se integrují podle jasného postupu, který není příliš zajímavý. Co třeba \sum_{n=1}^\infty\frac{1}{n^4}=\frac{\pi^4}{90}$)
\sum_{n=1}^\infty\frac{1}{n^4}=\frac{\pi^4}{90}$)
Offline
#6 30. 07. 2008 16:09
Re: Prázdninový integrál
Ten původní integrál lze vypočítat bez rozkladu na parciální zlomky a řešení soustavy rovnic. Výpočet integrálu se vleze na jeden max. dva řádky :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 30. 07. 2008 19:50 — Editoval Pavel (30. 07. 2008 19:52)
Re: Prázdninový integrál
↑ BrozekP:
ten výraz  ve jmenovateli mě přivádí na myšlenku pomoct si nějakou nekonečnou geometrickou řadou. Že by to bylo takhle?
ve jmenovateli mě přivádí na myšlenku pomoct si nějakou nekonečnou geometrickou řadou. Že by to bylo takhle?
$\int_0^\infty\frac{x^3}{e^x-1}\,\text{d}x=\int_0^\infty x^3(\frac 1{e^x}+\frac 1{e^{2x}}+\frac 1{e^{3x}}+\,\dots)\,\mathrm{d}x=\int_0^\infty x^3\sum_{j=1}^\infty e^{-jx}\,\mathrm{d}x=\int_0^\infty\sum_{j=1}^\infty x^3e^{-jx}\,\mathrm{d}x=\sum_{j=1}^\infty\int_0^\infty x^3e^{-jx}\,\mathrm{d}x=\sum_{j=1}^\infty\biggl([-\frac 1j\,x^3e^{-jx}]_0^{\infty}+\frac 3j\int_0^\infty x^2e^{-jx}\,\mathrm{d}x\biggr)=\nl= \sum_{j=1}^\infty\frac 3j\int_0^\infty x^2e^{-jx}\,\mathrm{d}x=\sum_{j=1}^\infty\biggl(\frac 3j\,[-\frac 1j\,x^2e^{-jx}]_0^{\infty}+\frac 6{j^2}\int_0^\infty xe^{-jx}\,\mathrm{d}x\biggr)=\sum_{j=1}^\infty\frac 6{j^2}\int_0^\infty xe^{-jx}\,\mathrm{d}x=\sum_{j=1}^\infty\biggl(\frac 6{j^2}\,[-\frac 1j\,xe^{-jx}]_0^{\infty}+\frac 6{j^3}\int_0^\infty e^{-jx}\,\mathrm{d}x\biggr)=\sum_{j=1}^\infty\frac 6{j^3}\int_0^\infty e^{-jx}\,\mathrm{d}x=\nl=\sum_{j=1}^\infty\frac 6{j^3}\,[-\frac 1j\,e^{-jx}]_0^{\infty}\,\mathrm{d}x=\sum_{j=1}^\infty\frac 6{j^4}=6\cdot\frac{\pi^4}{90}=\frac{\pi^4}{15}\,.$
Pozor na tu řadu, kterou uvádíš v nápovědě. Měla by tam být 4. mocnina.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 30. 07. 2008 20:12
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninový integrál
↑ Pavel:
Hezky jsi to vyřešil :-) Omlouvám se za chybu v nápovědě, kterou jsem převzal ze zdroje, z kterého jsem čerpal (http://www.karlin.mff.cuni.cz/~pokorny/fyz2.html), opravil jsem to, aby to nemátlo.
Opravdu mě ale nenapadá, jak ten tvůj integrál řešit jinak. Nechceš dát třeba malou nápovědu? :-)
Offline
#10 30. 07. 2008 20:16
Re: Prázdninový integrál
Stačí v čitateli něco přičíst a odečíst a jmenovatel vhodně upravit. Inspiraci najdeš v příspěvku od ↑ Jorica: :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#11 30. 07. 2008 20:33
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Prázdninový integrál
Taky nad tim dumam. Cely den. Po vzoru Poincareho jsem tomu rano venoval deset minut a pres den nechavam praci podvedomi :)
A protože se podvedomi dnes pekne flaka, tak jsem si rikal ze poprosim o radu:
Jde o to že se nějakou fintou udela rozklad na parcialni zlomky bez soustav rovnic pro neurcite koeficienty v citatelich, nebo je mozny prevod jeste do nejakeho uplne jineho tvaru, ktery je sikovny pro integrovani?
Parcialni zlomky jsou jista volba, to napadlo asi vetsinu ctenaru. Ale da to moc prace. Rikal jsem si jestli se neda najit neco co je v tomto pripade sikovnejsi, ale nic me nenapadlo. A to jsem trosku podvadel a nechal si spocitat tu primitivni funkci pocitacem :)
Offline
#12 30. 07. 2008 20:41 — Editoval jelena (31. 07. 2008 12:10)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prázdninový integrál
Zdravím vás :-)
Předně mám radost, že po "technické odmlce" píše Jorica, srdečný pozdrav:-)
Pavlovi udělim malou výchovnou poznámku - hodit jen tak zadání bez sdělení, co se očekává od ostatních.... to už, prosím, ne :-) - také jsi mohl dočkat pouze doporučení, a? použiješ wims nebo stránky pana Maříka.
Editace: víte, kdo to řekl?
Lze stanovit tyto zásady:
Když nikdo nežádá o radu, porada se nezačíná.
Když nikdo radu nevysloví, porada nepostupuje.
Když nikdo radu nevymezí, porada nedochází cíle.
- jinak integrál mám vyřešen polopatickou metodou (ale jen proto, že když jsem udělala rozklad - ručně :-) tak jsem byla příliš líná... a výsledek z wims říkal, že to půjde, tak jsem to dal neřešila přes zlomky, ale lopatou :-)
↑ BrozekP: - tady byl zajimavý postup od Mariana (k tvému zadání), na závěr v mém příspěvku je odkaz na "klasiku", kterou tady uvedl i kolega
Editace :-)
to bych si neodpustila, abych nepřidala pozdrav pro kaju.marika :-) V těch dnech zrovna připravuji jednoho budoucího studenta pro Vašeho strýčka (nebo pro některého z jeho kolegů) a pořad opakuji, aby dbal na úpravu výrazů :-) a dělení člen po členu.
Editace ještě jednou - pokus o opravu češtiny :-)
Offline
#13 31. 07. 2008 11:12
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninový integrál
↑ Pavel:
Já na to prostě nemůžu přijít. Jediné, co jsem schopen udělat je, že si v čitateli vytvořím výrazy tak, abych mohl zlomek roztrhnout a krátit, čímž se zase dostanu na parciální zlomky bez řešení soustavy rovnic. Jenže přitom využívám toho, že ten rozklad na parciální zlomky už znám a vím tedy jak čitatele upravovat :-)
Offline
#14 31. 07. 2008 11:43
Re: Prázdninový integrál
↑ BrozekP a ostatni interesovani:
Pokud mate zrovna maximalizovane okno s timto prispevkem, pak v pravem hornim rohu vaseho okna najdete tlacitko s jeho uzavrenim. Ne, nezavirejte. K tomuto znaku pridejte do exponentu vhodnou mocninu a zkuste radu od Pavla (pricist, odecist). Napovim jeste, ze vysledek se da zapsat podstatne jednoduseji, nez je jiz uvedeno.
Na tento integral se vaze jedna velice zajimava prihoda s couvanim nakladniho auta plne nalozeneho nejmenovanym pivem v jednom strmem svahu pod Lysou horou. Po vyreseni toho integralu velice jednoduchou metodou (viz ma napoveda) jsme s Pavlem nalezli analogii reseni uvedeneho integralu s dopravou piva pod Lysou horou. Ale o tom treba nekdy priste.
Offline
#15 31. 07. 2008 11:56 — Editoval jelena (31. 07. 2008 12:08)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prázdninový integrál
↑ Marian:
Zdravim, Mariane :-)
ten vysledek je skutecne kratsi - vcera overeno :-) pred kontrolou situace s pivem v Opavě (tady je vcelku rovina :-)
Offline
#16 31. 07. 2008 12:27
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninový integrál
Tak už jsem se konečně dobral k výsledku bez parciálních zlomků :-) Vychází mi  , jednodušší tvar už snad není možný :-)
, jednodušší tvar už snad není možný :-)
Offline
#17 31. 07. 2008 12:33 — Editoval Marian (31. 07. 2008 12:35)
Re: Prázdninový integrál
↑ BrozekP:
Ano, je to tak! Ten integral se da nalezt v Demidovicovi (v mem cislovani se jedna o ulohu c. 1920). To uz ted mohu klidne sdelit, protoze byste tam nelezli tentyz vysledek jako od BrozekP, takze skryvat neni ji co. Snad jen postup by nekdo jeste mohl zkusit. Ale to prenecham nekomu z resicich.
Offline
#19 31. 07. 2008 21:36
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Prázdninový integrál
↑ jelena:
Take zdravim a dekuji :)
Je to az neuvereni, zejmena po tom co jsme si letos v evaluacich nasich studentu precetli, ze na vysoke skole (zamereni na ekonomii) by se v matematice spis mely procvicovat procenta :)
Offline
#20 31. 07. 2008 22:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prázdninový integrál
↑ kaja.marik:
A budete tedy cvičit procenta?
To abych vědela, kterým směrem se mám ubírat (on, student, bude na provozně ekonomické fakultě :-) Já bych standardně "výrazy, elementární funkce, rovnice, nerovnice" a třeba je všechno jinak :-)
Offline
#21 31. 07. 2008 23:38 — Editoval kaja.marik (31. 07. 2008 23:41)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Prázdninový integrál
↑ jelena:
Tak tato fakulta se od pristiho semestru vymkla kontrole ustavu matematiky na lesnicke a drevarske fakulte a bude si matematiku ucit sama, lepe a ekonomicky. Jestli to znaci prechod od integralum k procentum zatim nevime :)
Ale pridal bych jeden link, ktery bude Vasemu studentovi uzitecny: www.pefka.net :) - ukradene zapoctove a zkouskove pisemky (i z matematiky), diskuse ke komu nechodit do cviceni protoze (probuh) chce aby u tabule pocitali i studenti a podobne pocteni ;)
Ale abych se vratil k integralu: ja a ani me podvedomi jsme ho nevyresili (teda, mysleno jinak nez pres parcialni zlomky), a je zajimave jak se mi to ted (kdyz znam vysledek) zda trivialni. To je to co me na matematice fascinuje :) viz (nejen) muj oblibeny vedec.
--------------------------------------------------------------------------------
Míjely tak dny, že Kája řekl: „Jako když strejček Fichtlovic bičem práská.“ Ty srpnové, ty už teprve ubíhaly, jak by je někdo popoháněl.
Offline
#22 01. 08. 2008 08:55
Re: Prázdninový integrál
↑ kaja.marik:
Kvuli me absenci jsem se Kajo ani nerozloucila s Tvym stryckem :-( Tak ho aspon pozdravuj. Jinak me zaujala pravdepodobna napln vyuky matematiky na PEFce..no procenta se kazdopadne muzou hodit, to je fakt ;-) A pokud se aspon pul semestru bude venovat jejich krasopisnemu psani, tim lip ? :-)))) No a k tomu, co vyzaduji nekteri ucitele (pocitani u tabule, atd.) tak to je vazne vrchol a k tomu neni co dodat :-)))
Offline
#23 01. 08. 2008 19:46
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninový integrál
Pouze doplním postup:
Substituce v druhém integrálu  ,
, 

Offline
#24 01. 08. 2008 20:11
Re: Prázdninový integrál
To je ono, výborně. Postup je opravdu elegantní :-) Jinak doplním, že na rozklad dvojčlenu  lze přijít jednoduchou úvahou. Protože
lze přijít jednoduchou úvahou. Protože  , je zřejmě, že
, je zřejmě, že  a
a 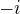 jsou komplexní kořeny uvedeného dvojčlenu. Tudíž je
jsou komplexní kořeny uvedeného dvojčlenu. Tudíž je  beze zbytku dělitelné dvojčlenem
beze zbytku dělitelné dvojčlenem  .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prázdninový integrál (TOTO TÉMA JE VYŘEŠENÉ)


 :-)
:-)