Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 13. 11. 2011 14:43
Re: Limita v krajních bodech def.oboru
↑ komar:
Ahoj. Jsem tu nová, ale doufám, že můj příspěvek pomůže.
Krajní body definičního oboru jsou +-0 a +- nekonečno.
počítejme limitu v bodě 0 zprava/zleva. Nejdříve doporučuji provést substituci y = 1/x, která převede případ na limitu pro y k +- nekonečno z fce  . Ta už se počítá dobře. Pro y v okolí minus nekonečna, je čitatel omezený a jmenovatel jde k do minus nekonečna, je tedy limita rovná 0. Pro y jdoucí k plus nekonečnu stačí použít L Hospitala, neboť čitatel i jmenovatel jdou k nekonečnu a dostaneme pak limitu pro y + nekonecno z fce
. Ta už se počítá dobře. Pro y v okolí minus nekonečna, je čitatel omezený a jmenovatel jde k do minus nekonečna, je tedy limita rovná 0. Pro y jdoucí k plus nekonečnu stačí použít L Hospitala, neboť čitatel i jmenovatel jdou k nekonečnu a dostaneme pak limitu pro y + nekonecno z fce  a to je nekonečno.
a to je nekonečno.
Podobně po stejné substituci v případě x = +- nekonečno, počítáme limitu pro y jdoucí k +- 0 z fce  . Čitatel je v okolí spojitý a omezený a jmenovatel jde k +- 0, takže výsledek je +- nekonečno
. Čitatel je v okolí spojitý a omezený a jmenovatel jde k +- 0, takže výsledek je +- nekonečno
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 13. 11. 2011 15:21
Re: Limita v krajních bodech def.oboru
↑ Andrejka3:
moc pomohla děkuji :-) a pomohla by jsi mi ještě prosím Tě. Potřeboval bych určit průsečíky s osami :-) nebo aspon radu :-)
Offline
#4 13. 11. 2011 15:30 — Editoval Andrejka3 (13. 11. 2011 15:31)
Re: Limita v krajních bodech def.oboru
↑ komar:
To jsem ráda. :)
Průsečíky:
S osou x: Zaprvé leží na ose x :) takže mají druhou souřadnici nulovou, tj. jsou tvaru [x,0]
Zadruhé jsou body té funkce, takže musí být f(x) = 0. Takže řešíš tuhle rovnici. Levá strana je součin dvou věcí - takže stačí, aby aspon jedna z nich byla nula. První člen,  , je ale vždy kladný, takže aby součin vyšel nula, musí být druhý činitel nulový, tj. x. Takže bychom psali, že [0,0] je hledaným průsečíkem, ale x = 0 je zakázané, není v definičním oboru. Průsečík s osou x neexistuje.
, je ale vždy kladný, takže aby součin vyšel nula, musí být druhý činitel nulový, tj. x. Takže bychom psali, že [0,0] je hledaným průsečíkem, ale x = 0 je zakázané, není v definičním oboru. Průsečík s osou x neexistuje.
S osou y: Zaprvé leží na ose y :) takže mají první souřadnici nulovou, tj. jsou tvaru [0,y]
Zadruhé jsou bodem té fce, tj. f(0) = y. Ale 0 není v definičním oboru f, takže f nemá ani průsečík s y.
What does a drowning number theorist say?
'log log log log ...'
Offline
#5 13. 11. 2011 18:43
Re: Limita v krajních bodech def.oboru
↑ Andrejka3:
ještě bojuji s Asymptotami poradíš ještě prosím :D :-)
Offline
#6 13. 11. 2011 19:31 — Editoval Andrejka3 (13. 11. 2011 19:35)
Re: Limita v krajních bodech def.oboru
↑ komar:
Asymptoty...
Podle definice, horizontální asymptota f pro x jdoucí do nekonečna je přímka: p(x) = ax +b taková, že
zaprvé lim (f - p)= 0 (pro x do nekonecna) a zároveň lim f/p = 1 pro x do nekonečna.
Analogicky pro x do minus nekonečna.
Lovím to z paměti.
Zkusme spočítat asymptotu pro x do nekonečna.
je lim f = nekonečno. Proto je jasné, že aby lim (f-p) = 0, musi byt lineární člen přímky kladný.
Počítáme lim (f/(ax+b)) =lim ( /(a+b/x)) = 1/a. To ma byt rovno 1, tedy a = 1.
/(a+b/x)) = 1/a. To ma byt rovno 1, tedy a = 1.
Dále taky má být lim (f-(x+b))=lim (x.( -1)-b) = lim x.(
-1)-b) = lim x.( -1) - b = 1 - b = ...0 takze b = 1.
-1) - b = 1 - b = ...0 takze b = 1.
Je tudiz p(x) = x + 1
Analogicky pro asymptotu v minus nekonecnu.
Kdybys nevěděl, jak na tu limitu, tak opět použij tu substituci, a pak to je přímo definice derivace exponenciály v bodě 0 (zprava ale to je fuk), což je jedna :)
What does a drowning number theorist say?
'log log log log ...'
Offline
#7 13. 11. 2011 21:16
Re: Limita v krajních bodech def.oboru
↑ Andrejka3:
asi by jsi mi to nemohla napsat na papir a poslat na email ze :( tedka jsem se uplne ztratil :(
Offline
#9 13. 11. 2011 21:57
Re: Limita v krajních bodech def.oboru
↑ Andrejka3:
strašně moc ti děkuji zítra to mám jet odevzdat a už nevím kdo by mi poradil. Kdyžtak toto je můj email pajikonupka@seznam.cz
Offline
#10 13. 11. 2011 22:02 — Editoval halogan (13. 11. 2011 22:59)
Re: Limita v krajních bodech def.oboru
↑ komar:
Mame funkci  .
.
Hledáme asymptoty. To jsou přímky, které dobře aproximují fci v okolí nekonečna.
Pokud existuje asymptota  fce
fce  pro
pro  , pak je jediná.
, pak je jediná.
Musí splňovat následující (podle toho se taky počítá): (1),
(1),
tedy funkční rozdíl v nekonečnu mizí a též (2)
(2)
tedy funkční hodnoty se přibližují dost rychle.
Rovnice přímky je  . Musíme ale najít neznámé
. Musíme ale najít neznámé 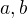 .
.
Dosadíme rovnici přímky a funkční předpis do rovnice (2). Levá strana vychází  . Pravá strana rovnice je 1. Odkud máme
. Pravá strana rovnice je 1. Odkud máme 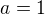 .
.
Potřebujeme dopočítat  . K tomu použijeme rovnici (1). Pišme levou stranu:
. K tomu použijeme rovnici (1). Pišme levou stranu: . Pravá strana rovnice je 0. Takže
. Pravá strana rovnice je 0. Takže  . Je to základní limita, nebo stačí použít l'Hospitala, nebo víme, že derivace exponencialy v nule je jedna a napíšeme definici. Každopádně,
. Je to základní limita, nebo stačí použít l'Hospitala, nebo víme, že derivace exponencialy v nule je jedna a napíšeme definici. Každopádně,  , tedy
, tedy  .\\
.\\
Chceme-li spočítat asymptotu  stejné fce pro okolí minus nekonečna, postupujeme analogicky, jen musíme změnit v (1) a (2) kam limitíme - do minus nekonecna.
stejné fce pro okolí minus nekonečna, postupujeme analogicky, jen musíme změnit v (1) a (2) kam limitíme - do minus nekonecna.
Měj se.
edit: jen oprava závorky
What does a drowning number theorist say?
'log log log log ...'
Offline

 ,0)
,0) (0,+
(0,+