Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 11. 2011 15:41 — Editoval Klainer (12. 11. 2011 16:39)
Princip inkluze a exkluze
Dobrý den, nevím si ted rady s dvouma příklady na princip inkluze a exkluze:
1) Kolik existuje surjekcí n-prvkové množiny na (n-1) prvkovou množinu.
2) Jandě zbylo od narozenin 6 čokoládových bonbonů. Chce je rozdělit na 4 po sobě jdoucí dny tak, aby každý den snědla alespoň jeden.Kolik má možností ?
a) Pokud je 6 bonbónů různých ?
b) Pokud je 6 bonbonu stejných ?
Za a) Jsem vypočítal viz obr: 
Bohužel mě nenapadá způsob jak vypočítat variantu b, když mám všechny bonbony stejné.
Děkuji mockrát za rady a Váš čas !
Offline
#2 12. 11. 2011 16:07 — Editoval OiBobik (12. 11. 2011 16:08)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Princip inkluze a exkluze
↑ Klainer:
Nazdar,
když máš všechny bonbony stejné, tak jediné, čím se jednotlivé způsoby rozdělení liší, je počtem bonbonů, snězených v ten který den. Tedy každý validní způsob požírání dovedu vystihnout popsat právě jednou uspořádanou čtveřicí  kladných celých čísel takových, že
kladných celých čísel takových, že 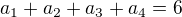 . To je celkem typová úložka ; ))
. To je celkem typová úložka ; ))
Pokud jsi ji zatím nikdy neviděl, zkus se zamyslet, jak lze zakódovat zase tyto čtveřice - představ si, že máš v řadě nějaké tři děliče mezi čtyřmi přihrádkami, mezi které máš rozmístit 6 nerozeznatelných kuliček tak, aby mezi každými dvěma děliči (a i na krajích řady) byla vždy alespoň jedna kulička.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 12. 11. 2011 16:14
Re: Princip inkluze a exkluze
a) souhlas
b) protože každý den alespoň jeden bonbón, tak bych prostě 4 bonbóny odečet, a zjišťoval, kolika způsoby lze sníst 2 bonbóny ve 4 dnech.
Představ si den jako čárku, a bonbón jako kuličku. Potom každý možný uspořádání se dá zobrazit jako např.  , kde první den by nesnědla nic, druhý 1, třetí 1, čtvrtý nic. Nebo
, kde první den by nesnědla nic, druhý 1, třetí 1, čtvrtý nic. Nebo  , kdy čtvrtý den snědla oba. Takže to je množina o 5 prvcích, a nás zajímá počet dvouprvkových podmnožin.
, kdy čtvrtý den snědla oba. Takže to je množina o 5 prvcích, a nás zajímá počet dvouprvkových podmnožin.
Offline
#4 12. 11. 2011 16:32 — Editoval Klainer (12. 11. 2011 18:05)
Re: Princip inkluze a exkluze
Tak jsem na to šel takhle:
mám 4 přihrádky - dny mezi tyto přihrádky dávám 6 bonbonu. Ošetření toho aby byl vždy mnimálně 1 bonbon jsem udělal takhle:
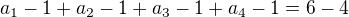
Substituce: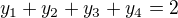
A pak počítám kombinace s opakováním: 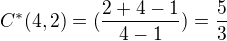
To lomítko tam nemá byt a vychází mi to 10.
Počítám to správně :) ? Pokud ano, neví někdo ještě jak na ten první příklad ?
1) Kolik existuje surjekcí n-prvkové množiny na (n-1) prvkovou množinu.
Offline
#5 13. 11. 2011 12:19
Re: Princip inkluze a exkluze
↑ Klainer:Ano, část b) je nyní správně.
Pozn.: Kombinační čísla se dají napsat pomocí {n \choose k} v dolarech.
Offline