Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 11. 2011 13:35
limita
Nazdar, prosim vas, robi mi problem vyratat limitu tohto vyrazu pre x->(0-). Skusal som pouzit 2x L´Hospitala, ale aj tak ked dosadim potom 0- tak mi vyjde nekonecno/0. Neviem ako postupovat. Vysledna limita by mala byt nekonecno.
Offline
- (téma jako vyřešené označil(a) kefnas)
#4 15. 11. 2011 14:31 — Editoval stenly (15. 11. 2011 14:35)
Re: limita
↑ kefnas:Limita vyjde nula viz důkaz výše.Jen tam mám drobnou chybu v konci,kde e na 00*00=00.Čitatel je 2 a jmenovatel 00.Z toho celá limita je po dvojím Lopitalu rovna nule.
Matematika je způsob,jak zviditelnit neviditelné!!
Offline
#6 15. 11. 2011 14:34
Re: limita
↑ stenly:
Ale v menovateli mas prvu cast dobre, e^nekonecno*nekonecno moze byt....ale potom je tam + e^nekonecno*0...a z toho svorka ze to je 0, ale nie je. Wolfram vypocital ze tato lim ma byt nekonecno, nie nula. Cize isto to takto nie je. http://www.wolframalpha.com/input/?i=li … 2F2x%29%29
Offline
#8 15. 11. 2011 21:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita
↑ stenly:, ↑ kefnas:
Zdravím vás,
zápornou reputaci udělenou kolegou Kefnas kolegovi Stenly jsem smazala. Znění:
kenfas v reputaci pro stenly napsal(a):
neochota pomoct v danej problematike
mi nepřišlo přiměřené k vývoji v tématu. Pokud jste se dostali do matematického sporu v řešení matematické úlohy, tak to laskavě vyřešte slušnou matematickou debatou a matematickými argumenty. Děkuji za pochopení.
K problému - nejeví se mi, že pomoci l´Hospital se dá dostat k výsledku, ale je to jen rychlý náhled, děkuji, pokud se objeví podrobné odůvodnění.
Offline
#10 15. 11. 2011 23:48
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita
↑ Alesak:
děkuji, tak úplně průkazné se mi to nezdá (jen pocitově - což je málo :-) - nerozepsal bys podrobně, pokud čas dovolí? Jinak nechám to ještě otevřené. Zdravím.
Offline
#11 16. 11. 2011 10:14
Re: limita
↑ jelena:
Na tohle je nějaká věta, pánové to určitě dohledají ve svých skriptech, jestli budou chtít:) Postup důkazu by asi zahrnoval to přepsat pomocí taylorova rozvoje na součin nebo podíl dvou polynomů.
Napadla mě ještě tahle úprava:
Offline
#12 16. 11. 2011 10:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita
↑ Alesak:
děkuji, zdá se že v takové úpravě vypadlo  před log v závorce (a minus v úvodním zápisu - jen překlep)
před log v závorce (a minus v úvodním zápisu - jen překlep) 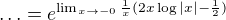 . Je tak? Děkuji (nedaří se mi v tom uvidět úplně průkazný zápis a navíc to momentálně nezapadá do mého plánu).
. Je tak? Děkuji (nedaří se mi v tom uvidět úplně průkazný zápis a navíc to momentálně nezapadá do mého plánu).
Za další nápady děkuji.
Offline
#13 16. 11. 2011 11:03
Re: limita
↑ jelena:
Jestli se hodí, můžeme udělat následující:
místo limity pro x ->0- pocitat lim pro y->-nekonecno, prevedenim promenne y=1/x. Pak totiz staci dvakrat pouzit l'Hospitala: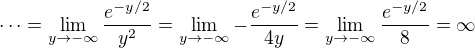 .
.
What does a drowning number theorist say?
'log log log log ...'
Offline
#15 16. 11. 2011 22:34
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita
↑ Andrejka3:, ↑ Alesak:
děkuji vám, oba postupy už mi smysl dávají.
----------------------------------
OT: ↑ Alesak: :-) sleduj, jak se starám o Tvé téma (každý rok (až na 2009) ho oprašuji (a tak pěkně se rozrůstá) - už by se toho mohl ujmout někdo jiný)
Offline

 re]
re]