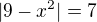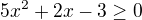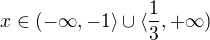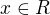Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 31. 07. 2008 14:39 — Editoval lukaszh (31. 07. 2008 21:08)
Re: Kvadratické rovnice/nerovnice
↑ JohnBe:
1. Zapíšem si to v tvare 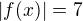 , potom urcis nulove body
, potom urcis nulove body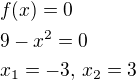
Tieto body ti rozdelia definičný obor na tri intervaly: 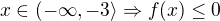 , potom
, potom 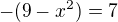
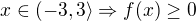 , potom
, potom 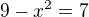
 , potom
, potom 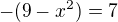
Vyriesis rovnice, len pozor na intervaly. Riesenia sa musia nachadzat v danom intervale.
2. Vyjmes pre zatvorku x:
Podla definicie:![kopírovat do textarea $[(x<0)\wedge(x-7>0)]\vee[(x>0)\wedge(x-7<0)] \nl [(x<0)\wedge(x>7)]\vee[(x>0)\wedge(x<7)]\nl \empty\cup(0;7)=(0;7)$](/mathtex/1a/1acc0e680b4c7e37e14233424a7ef011.gif)
Opravené ... ;-)
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 31. 07. 2008 15:01 — Editoval Marian (31. 07. 2008 15:01)
Re: Kvadratické rovnice/nerovnice
↑ lukaszh: V poslednim radku ma byt znak konjunkce (v), nikoliv mnozinove sjednoceni (u), popr. nech sjednoceni, ale odstran hranate zavorky.
Offline
#5 06. 08. 2008 11:12
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Kvadratické rovnice/nerovnice
↑ Zbyšek:
U toho prního nestačí říct, že má nekonečně mnoho řešení (např. v intervalu (0,1) je nekonečně mnoho řešení, ale nejsou všechna), řešením jsou všechna reálná čísla. Druhý OK.
Offline
#6 06. 08. 2008 11:31
Re: Kvadratické rovnice/nerovnice
↑ Zbyšek:
hovorime tady o rovnicich nebo nerovnicich? A jaky je tady obor nezname x. To jsou zcela urcujici faktory, bez nichz nelze seriozne diskutovat. A co to znamena jakehokoliv cisla? I komplexniho, protoze pak musim oponovat i BrozekP, ktery pravdepodobne uvazuje pouze realna cisla, jak se da predpokladat na vetsine SŠ. Ale pravidlo to jiste neni.
Offline
#7 06. 08. 2008 19:34
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Kvadratické rovnice/nerovnice
↑ Marian:
Zcela souhlasím. Uvažoval jsem pouze reálná čísla, protože se takto příklady na střední škole obvykle zadávají a Zbyšek neuvedl jinak, měl jsem na to upozornit. V oboru komplexních čísel nerovnice řešení má.
Offline
#9 07. 08. 2008 21:09 — Editoval Marian (08. 08. 2008 00:32)
Re: Kvadratické rovnice/nerovnice
↑ Zbyšek:
Ad 1. S diskriminantem D=64 souhlasím, také kořeny jsou vypočítány správně. Vzhledem k tomu, že koeficient u nejvyšší mocniny je kladný (a=5), je skutečně nerovnice splněna pro všechna reálná čísla intervalu 
Ad 2. Také zde je to správně. Metoda může být stejná jako v případě (1), nicméně s výhodou lze uvážit vytknutí a řešení v součinovém tvaru.
Poprosil bych jen trošku přepsat výrazy v TeXu; správně se to píše takto:
Code:
x\in(-\infty ,-1\rangle\cup\langle\frac{3}{5},+\infty )Dostaneš pak
Offline
#11 08. 08. 2008 00:30 — Editoval Marian (08. 08. 2008 00:32)
Re: Kvadratické rovnice/nerovnice
↑ Zbyšek:
Ad 1. S první úlohou souhlasím.
Ad 2. Nalezení kořenů v druhé úloze je v pořádku (dostaneš dvojnásobný kořen x=1). Dá se to řešit ale i tak, že si všimneš na začátku, že lze napsat
Odtud je vidět snadno řešení. Má totiž platit  . Tady ale máš chybu, nebo? nelze brát v potaz hodnotu x=1 (tedy kořen kvadratického trojčlenu na levé straně nerovnice). Správné řešení je tedy
. Tady ale máš chybu, nebo? nelze brát v potaz hodnotu x=1 (tedy kořen kvadratického trojčlenu na levé straně nerovnice). Správné řešení je tedy 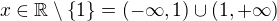 . Sám uvaž, jak by vypadalo řešení v případě že by v zadání byl neostrý znak nerovnosti, tedy znak
. Sám uvaž, jak by vypadalo řešení v případě že by v zadání byl neostrý znak nerovnosti, tedy znak  .
.
Ad 3. Trojka je správně, tedy 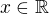 .
.
Offline