Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Další izomorfní algebry (TOTO TÉMA JE VYŘEŠENÉ)
#26 19. 11. 2011 14:36
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑↑ Andrejka3:
Píšeš, že 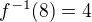 . Ale
. Ale 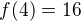 .
.
Offline
#28 19. 11. 2011 14:38
Re: Další izomorfní algebry
↑ Pavel Brožek:
No tak to je v pytli.
What does a drowning number theorist say?
'log log log log ...'
Offline
#29 19. 11. 2011 14:42
Re: Další izomorfní algebry
Ahoj↑↑ Pavel Brožek:,
A co sa stane ak i=2 (inac i>=2)?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#30 19. 11. 2011 14:48
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ vanok:
Nerozumím, co by se mělo stát. Např.
Offline
#31 19. 11. 2011 14:50
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
Proč? Odvodit ten vztah je úplně jednoduché. Stačí složit isomorfismus 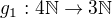 s isomorfismem
s isomorfismem 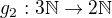 , přičemž isomorfismy g používám přesně takové, jaké jsme tu popsali pro nesoudělná čísla.
, přičemž isomorfismy g používám přesně takové, jaké jsme tu popsali pro nesoudělná čísla.
Offline
#32 19. 11. 2011 14:50 — Editoval Andrejka3 (19. 11. 2011 14:52)
Re: Další izomorfní algebry
↑ Pavel Brožek:
Takže myslíš si, že to je v pořádku? Že jsme to udělali dobře?
Zrovna jím a budu mít prostor na pořádné psání až kolem večera.
Edit: Tak fajn, to jsem ráda, mám zase povznesenou náladu:)
What does a drowning number theorist say?
'log log log log ...'
Offline
#33 19. 11. 2011 14:55 — Editoval vanok (19. 11. 2011 15:02)
Re: Další izomorfní algebry
↑ Pavel Brožek:, to preto ze si pisal (i mod2), v tvojom vzorci, vidim teraz ako to chapat.
A este f(8) a f(4) su rozne ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#34 19. 11. 2011 15:00
Re: Další izomorfní algebry
↑ Andrejka3: dakujem
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#35 19. 11. 2011 15:00
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ vanok:
Tím jsem myslel zbytek po dělení i dvěma. To tedy nijak neomezuje i.
↑ Andrejka3:
Dá se snadno určit i inverzní zobrazení 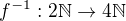

a dá se ověřit, že složení 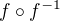 je identita.
je identita.
Já věřím, že jsme nikde neudělali chybu :-). Ale kdyby to ještě někdo potvrdil, byl bych rád.
Offline
#36 19. 11. 2011 15:05
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ vanok:
Takže jsou různé.
Offline
#37 19. 11. 2011 15:14
Re: Další izomorfní algebry
↑ Pavel Brožek:, ok. Dakujem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#38 19. 11. 2011 15:26 — Editoval Pavel Brožek (19. 11. 2011 15:37)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
Tak se zdá, že to nefunguje :-(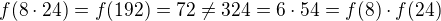
Edit: Problém je už v tom, že neplatí ↑↑ toto: (platilo by to, kdyby a bylo nesoudělné s m a n, jenže to nejde zaručit). Takže jsme zase skoro na začátku…
Offline
#39 19. 11. 2011 16:32
Re: Další izomorfní algebry
↑ Pavel Brožek:
Ve sbírce není napsané řešení.
Uvidíme, třeba na to ještě přijdeme.
What does a drowning number theorist say?
'log log log log ...'
Offline
#40 19. 11. 2011 16:54 — Editoval Pavel Brožek (19. 11. 2011 17:07)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
Domněnka (z velké části shodná s tím, co uvádíš v prvním příspěvku):
Pokud čísla m a n mají prvočíselné rozklady ( je i-té prvočíslo, tj.
je i-té prvočíslo, tj. 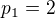 ,
, 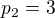 a tak dále)
a tak dále)
(od určitého indexu tedy budou r a s nulová) a existuje bijekce  taková, že
taková, že  pro každé
pro každé  , pak funkce
, pak funkce 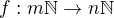
taková, že
je isomorfismus.
Offline
#41 19. 11. 2011 17:18
Re: Další izomorfní algebry
↑ Pavel Brožek:
Ona se liší v tom, že povoluješ, aby v rozkladu byla třeba 2 u obou čísel i s jinou mocninou, že?
Společná prvočísla nemusí mít stejnou mocninu.
What does a drowning number theorist say?
'log log log log ...'
Offline
#42 19. 11. 2011 17:29
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
Ano, přesně tak.
Snažil jsem se to také zformulovat tak, aby nebylo těžké dokázat, že to je isomorfismus.
Offline
#43 19. 11. 2011 17:59
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
Napadl mě trochu nový pohled na věc.
Mějme danou posloupnost nezáporných celých čísel 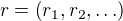 s konečným počtem nenulových členů. Pak definujme algebru
s konečným počtem nenulových členů. Pak definujme algebru 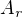 takovou, že její prvky budou všechny posloupnosti
takovou, že její prvky budou všechny posloupnosti  nezáporných čísel takových, že
nezáporných čísel takových, že 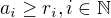 a počet nenulových
a počet nenulových  je konečný. Operaci + definujme jako běžné sčítání posloupností.
je konečný. Operaci + definujme jako běžné sčítání posloupností.
Ukažme nyní, že algebra 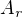 je isomorfní algebře
je isomorfní algebře 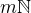 , kde
, kde  . Budeme ověřovat, že isomorfismem je následující zobrazení
. Budeme ověřovat, že isomorfismem je následující zobrazení 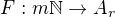 :
:
Jestliže je  , pak jeho prvočíselný rozklad můžeme napsat jako
, pak jeho prvočíselný rozklad můžeme napsat jako 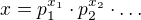 , kde
, kde 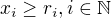 . Číslu
. Číslu  pak přiřadíme posloupnost
pak přiřadíme posloupnost  .
.
Je snad evidentní, že f je bijekce. Dokažme tedy, že zachovává operaci.
Převedl jsem tak problém na to, že máme zjistit, pro jaké různé posloupnosti r a s jsou algebry 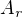 a
a 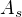 isomorfní. Z tohoto pohledu se zdá tvrzení ↑ Pavel Brožek: skoro triviální.
isomorfní. Z tohoto pohledu se zdá tvrzení ↑ Pavel Brožek: skoro triviální.
Offline
#44 19. 11. 2011 18:31
Re: Další izomorfní algebry
↑ Pavel Brožek:
Hezké.
Například algebra 2N je izomorfní algebře posloupností, jež mají první člen větší nebo roven jedné.
Algebra 4N je izomorfní algebře posl., jež mají první člen větší nebo roven dvěma. Hmmm.
Pravda, že usnadní tento pohled důkazu toho tvrzení.
Myslela jsem, že mě teď napadne třeba důvod proč (ne)jsou výše zmíněné algebry izomorfní.
Napsala jsem to správně?
What does a drowning number theorist say?
'log log log log ...'
Offline
#45 19. 11. 2011 18:32
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
Ano, tak je to myšlené. Zdá se mi ale, že to jen usnadňuje najít ty isomorfismy, ale nevím, jestli to bude užitečné k důkazu, že isomorfismus neexistuje.
Offline
#46 19. 11. 2011 18:42
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
Už jen spíš drobnost:
Každá algebra 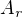 je isomorfní nějaké algebře
je isomorfní nějaké algebře 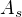 , kde s je nerostoucí posloupnost (to tvrdím na základě ↑ Pavel Brožek:). Můžeme tak zkoumat jen algebry
, kde s je nerostoucí posloupnost (to tvrdím na základě ↑ Pavel Brožek:). Můžeme tak zkoumat jen algebry 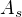 , kde s je nerostoucí. Mohlo by se ukázat, že libovolné dvě různé takové algebry nebudou isomorfní.
, kde s je nerostoucí. Mohlo by se ukázat, že libovolné dvě různé takové algebry nebudou isomorfní.
Offline
#47 19. 11. 2011 18:45
Re: Další izomorfní algebry
Este jeden problem: Teraz mi napadlo ci existuju nejake automorfismy v takychto strukturach?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#48 19. 11. 2011 19:01 — Editoval Andrejka3 (19. 11. 2011 19:08)
Re: Další izomorfní algebry
↑ Pavel Brožek:
Jo takto :)
Nad tím jsem dumala docela dlouho než mi to došlo.
Ad Vanok:
Automorfismy jsou, pokud si dobře pamatuji, bijektivní endomorfismy, tj. isomorfismy na stejný nosič?
Každopádně, kdyby někdo hledal tu sbírku nebo hezký výklad algebry, doporučuji
heslo google: trlifaj Nalg026
popř. algebra sbírka nebo tak něco.
EDIT: Vlastně není mi jasné, že je jednoduché dokázat, že jiné algebry nejsou izomorfní.
What does a drowning number theorist say?
'log log log log ...'
Offline
#49 19. 11. 2011 19:08
Re: Další izomorfní algebry
↑ Andrejka3:,
Ano.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#50 19. 11. 2011 19:22
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
To já také nevím, jak dokázat, že jsou jiné neisomorfní. Jen bych to trochu čekal, proto jsem se snažil problém přeformulovat tak, aby všechny algebry, které budeme uvažovat, byly neisomorfní. Je možné, že se ukáže, že některé (možná i všechny) isomorfní jsou.
Založil jsem téma, které by nám možná mohlo pomoct.
Offline
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Další izomorfní algebry (TOTO TÉMA JE VYŘEŠENÉ)