Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Bijekce podmnožin přirozených čísel (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 11. 2011 19:19 — Editoval Pavel Brožek (19. 11. 2011 20:03)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Bijekce podmnožin přirozených čísel
Pro  definujme množiny
definujme množiny
Určtete, pro které dvojice  (
( ) existuje bijekce
) existuje bijekce  taková, že platí
taková, že platí  pro všechna
pro všechna  , případně najděte takovou bijekci.
, případně najděte takovou bijekci.
(Inspirace k úloze pochází odtud.)
Offline
- (téma jako vyřešené označil(a) Pavel Brožek)
#2 19. 11. 2011 19:59
Re: Bijekce podmnožin přirozených čísel
Ahoj ↑ Pavel Brožek:,
A f je len banalna bijekcia ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 19. 11. 2011 20:01 — Editoval Pavel Brožek (19. 11. 2011 20:03)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Bijekce podmnožin přirozených čísel
↑ vanok:
Ahoj,
musí splňovat  , takže bych ji nenazýval banální (pokud tedy „banální“ není matematický pojem, který neznám).
, takže bych ji nenazýval banální (pokud tedy „banální“ není matematický pojem, který neznám).
Edit: Upravil jsem, že rovnost musí platit pro všechna  .
.
Offline
#4 19. 11. 2011 20:52
Re: Bijekce podmnožin přirozených čísel
↑ Pavel Brožek:,
Dakujem prave to som chcel vediet.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 19. 11. 2011 22:45
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: Bijekce podmnožin přirozených čísel
↑ Pavel Brožek:
Ahoj. Jaký je prosím vztah algeber 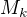 (uvedené zde) a
(uvedené zde) a 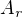 (uvedené v odkazovaném tématu)? A nebo není toto téma motivováno odvozením vlastností
(uvedené v odkazovaném tématu)? A nebo není toto téma motivováno odvozením vlastností 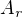 ? - S jakou strukturou v původním tématu je potom izomorfní
? - S jakou strukturou v původním tématu je potom izomorfní 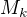 ? Děkuji.
? Děkuji.
"Máte úhel beta." "No to nemám."
Offline
#6 19. 11. 2011 22:58 — Editoval Pavel Brožek (19. 11. 2011 22:58)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Bijekce podmnožin přirozených čísel
↑ check_drummer:
Ahoj. Bylo to myšleno tak, že pokud dokážeme vyřešit tuto úlohu, tak pak budeme mít snad blíže k vyřešení odkazované úlohy.
Pokud si vezmeme množinu 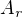 , tak pro každé
, tak pro každé  a každou posloupnost
a každou posloupnost  bude
bude 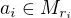 . Pokud bychom nalezli obecně isomorfismus
. Pokud bychom nalezli obecně isomorfismus  , pak by bylo snadné sestrojit isomorfismus
, pak by bylo snadné sestrojit isomorfismus  algeber
algeber 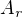 a
a 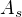 pomocí isomorfismů
pomocí isomorfismů  takto:
takto: 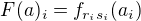 . Snad jsem to nepopletl.
. Snad jsem to nepopletl.
Chtěl jsem ale tuhle úlohu pojmout nezávisle na té odkazované. (Řešení už znám, tedy alespoň myslím.)
Offline
#7 20. 11. 2011 12:43 — Editoval FailED (20. 11. 2011 12:48)
Re: Bijekce podmnožin přirozených čísel
Offline
#8 20. 11. 2011 15:08
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Bijekce podmnožin přirozených čísel
↑ FailED:
Ahoj,
já jsem postupoval trochu jinak (komplikovaněji).
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Bijekce podmnožin přirozených čísel (TOTO TÉMA JE VYŘEŠENÉ)
 , pak
, pak 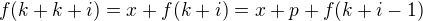 pro
pro  , abychom dostali bijekci, musí být
, abychom dostali bijekci, musí být 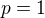 a proto i
a proto i  , dále
, dále  , tedy nutně
, tedy nutně  a to je spor.
a to je spor. , která číslu
, která číslu  přiřadí počet uspořádaných dvojic z příslušné množiny
přiřadí počet uspořádaných dvojic z příslušné množiny  takových, že součet dvojice je číslo
takových, že součet dvojice je číslo  v
v  , protože existují tři rozklady čísla 8:
, protože existují tři rozklady čísla 8:  ,
,  a
a  .
. v
v  v
v  a pro žádné jiné prvky
a pro žádné jiné prvky  a z toho
a z toho 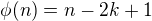 v
v  . Přitom ale
. Přitom ale  . Dohromady a po dosazení
. Dohromady a po dosazení  :
: