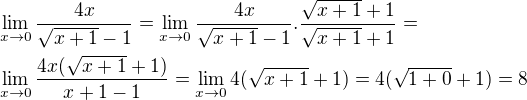Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 11. 2011 10:45
- michaela20

- Zelenáč
- Příspěvky: 8
- Reputace: 0
Limity
Dobrý den, nenašla by se dobrá duše, která si ví rady s těmito příklady?? Jsem v koncích..
lim (x> 0)=(sin4*x)/(sqrt(x+1)-1)
a
lim (x> 0-) = (sqrt(1-cos2*x)/x)
děkuji
Offline
- (téma jako vyřešené označil(a) michaela20)
#3 22. 11. 2011 11:24
- michaela20

- Zelenáč
- Příspěvky: 8
- Reputace: 0
Re: Limity
↑ Alivendes:
Moc děkuji, já jsem si to taky rozšířila, ale dál jsem si nebyla moc jistá, jestli to takhle můžu dělat.
Offline
#4 22. 11. 2011 11:27
Re: Limity
↑ michaela20:
Musí se to takhle dělat:)
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#5 22. 11. 2011 11:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ michaela20:
děkuji za nové téma, také je vhodné doplnit, že takové doporučení nepomohlo. Děkuji.
↑ Alivendes:
Zdravím,
nemám čas teď zkoumat jaké jsou novinky v oboru vyšetřování limit, ale předpokládám, že platí nějaké "věty" (jak bylo použito?).
Co znamená takové tvrzení:
Fuknci sinus můžeme v okolí bodu nula aproximovat přímkou:
a
Musí se to takhle dělat:)
Děkuji.
Offline
#6 22. 11. 2011 16:31 — Editoval Alivendes (22. 11. 2011 17:25)
#7 22. 11. 2011 22:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ Alivendes:
máme v zadání podíl funkcí, každá z těchto funkci v bodě 0 má limitu vlastní a to 0. Tedy dostali jsme neurčitý výraz 0/0 a je třeba zvolit jinou cestu, než přimočáré požití věty o limitě podílu funkcí.
Proto provádíme úpravu, která umožní použit jednu z pozoruhodných limit a větu o součinu limit (a to rozšíření zlomku):
Teď upravím limitu součinu funkcí na součin limit: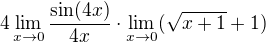
1. limita je tabulková, 2. limita se určí dosazováním (takovou radost nám však zadavateli... (c))
Snad nedostanu kritiku od limito-autorit, pro jistotu děkuji :-)
Offline
#8 22. 11. 2011 22:36 — Editoval Alivendes (22. 11. 2011 22:38)
Re: Limity
↑ jelena:
Děkuji, vyšlo nám to stejně, delší dobu používám tenhle způsob. V tom tvém vidím ten správný ,,matematický pořádek,,.
Ale přijde mi to jako dobrý trik, co proti tomu máš ?
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#9 22. 11. 2011 22:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
kolega Alivendes napsal(a):
Ale přijde mi to jako dobrý trik, co proti tomu máš ?
Musel bys mi ukázat, jak je odvozen nebo oficiálně zdůvodněn, například v které knize je uveden. Ale bude nejlepší, pokud Tvůj postup posoudí někdo s opravdu matematickou přípravou. Děkuji.
Offline

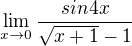
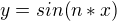 platí, že se v okolí bodu nula chová jako přímka
platí, že se v okolí bodu nula chová jako přímka