Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Další izomorfní algebry (TOTO TÉMA JE VYŘEŠENÉ)
#51 19. 11. 2011 22:49
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
Tvrzení 1
Pro prvek  z algebry
z algebry  označme
označme 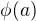 počet uspořádaných dvojic
počet uspořádaných dvojic  (
(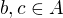 ) takových, že
) takových, že 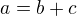 . Jestliže je algebra
. Jestliže je algebra  isomorfní s algebrou
isomorfní s algebrou  a
a  je isomorfismus algeber, pak platí
je isomorfismus algeber, pak platí 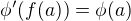 (
(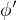 je definována jako
je definována jako  , jen působí na algebře
, jen působí na algebře  ).
).
Důkaz Tvrzení 1
Tvrzení bude dokázáno, pokud najdeme bijektivní zobrazení (označme ho g) mezi všemi dvojicemi  takovými, že
takovými, že 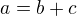 a mezi všemi dvojicemi
a mezi všemi dvojicemi  takovými, že
takovými, že 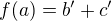 . Ukažme, že
. Ukažme, že  je takovým zobrazením, tedy že obrazy splňují požadovanou podmínku, g je prosté a na.
je takovým zobrazením, tedy že obrazy splňují požadovanou podmínku, g je prosté a na.
Obrazy splňují požadovanou podmínku, protože platí 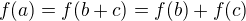 .
. je prosté zobrazení, protože f je prosté zobrazení.
je prosté zobrazení, protože f je prosté zobrazení. je na, protože pro každou dvojici
je na, protože pro každou dvojici  platí
platí 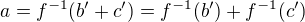 , má tedy svůj vzor
, má tedy svůj vzor 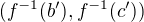 .
.
____________________________________
Teď se vraťme k našim algebrám 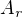 , kde
, kde  je nerostoucí posloupnost. Asi nemusím nějak více rozvádět, že pro
je nerostoucí posloupnost. Asi nemusím nějak více rozvádět, že pro 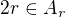 platí
platí 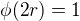 (protože
(protože  ) a že pro žádný jiný prvek
) a že pro žádný jiný prvek  rovnost
rovnost  neplatí. Isomorfismus
neplatí. Isomorfismus 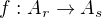 tedy podle Tvrzení 1 musí splňovat
tedy podle Tvrzení 1 musí splňovat 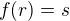 .
.
Tvrzení 2
Pro  a
a 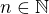 ,
, 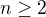 platí
platí 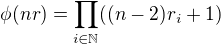 .
.
Důkaz Tvrzení 2
Jestliže chceme posloupnost 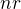 rozložit na součet dvou posloupností
rozložit na součet dvou posloupností  , musí pro každý prvek posloupnosti platit
, musí pro každý prvek posloupnosti platit 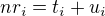 . Posloupnosti
. Posloupnosti  a
a  jsou z algebry
jsou z algebry 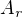 , platí proto
, platí proto 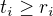 a
a 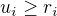 . Můžeme volit
. Můžeme volit 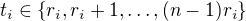 , to je celkem
, to je celkem 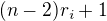 voleb. Takto můžeme volit rozklady nezávisle pro všechny
voleb. Takto můžeme volit rozklady nezávisle pro všechny  . Počet rozkladů je proto
. Počet rozkladů je proto  .
.
____________________________________
Platí 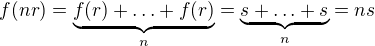 a tedy
a tedy 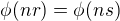 , přepsáno pomocí Tvrzení 2
, přepsáno pomocí Tvrzení 2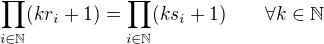
(Provedl jsem posunutí  a navíc vyloučil případ
a navíc vyloučil případ 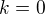 , protože je triviální a nic neříká.)
, protože je triviální a nic neříká.)
Mějme pevně dány posloupnosti  a
a  . Musí existovat číslo
. Musí existovat číslo 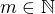 takové, že
takové, že 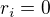 a
a 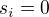 pro
pro  . Nekonečný součin (který ale byl vždy dobře definovaný, protože se od jistého i násobily jen jedničky) můžeme přepsat
. Nekonečný součin (který ale byl vždy dobře definovaný, protože se od jistého i násobily jen jedničky) můžeme přepsat
Na levé straně máme polynom v  a ten se rovná nule. Kdyby všechny koeficienty polynomu nebyly nulové, tak by to znamenalo, že máme polynom konečného nenulového řádu, který má nekonečně mnoho kořenů, což je evidentní spor. Každý koeficient tedy musí být nulový. Dostáváme tak sadu rovnic
a ten se rovná nule. Kdyby všechny koeficienty polynomu nebyly nulové, tak by to znamenalo, že máme polynom konečného nenulového řádu, který má nekonečně mnoho kořenů, což je evidentní spor. Každý koeficient tedy musí být nulový. Dostáváme tak sadu rovnic
To je velké omezení, posloupnosti 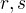 , které nesplňují každou z uvedených rovností, nemohou vytvořit isomorfní algebry
, které nesplňují každou z uvedených rovností, nemohou vytvořit isomorfní algebry  . Je možné, že soustava rovnic dokonce implikuje
. Je možné, že soustava rovnic dokonce implikuje  , tak daleko jsem se ještě nedostal.
, tak daleko jsem se ještě nedostal.
(Trochu mě tento příspěvek vyčerpal, tak se mi ho teď nechce moc důkladně kontrolovat, omluvte prosím případné chyby :-) ).
Offline
#52 19. 11. 2011 23:27
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
Dokončení důkazu:
Sestavme polynom
Jeho kořeny jsou podle Vietových vzorců čísla 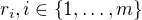 . Polynom
. Polynom
má však úplně stejné koeficienty, proto má také stejné kořeny. Množina všech  a množina všech
a množina všech  jsou proto shodné až na permutaci, která nás však nezajímá, protože
jsou proto shodné až na permutaci, která nás však nezajímá, protože  a
a  jsou neklesající posloupnosti. Máme tedy výsledek
jsou neklesající posloupnosti. Máme tedy výsledek  .
.
Tím je vše dokončeno a pro daná čísla  a
a  z původního zadání už umíme rozhodnout, zda jsou
z původního zadání už umíme rozhodnout, zda jsou 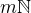 a
a 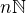 isomorfní.
isomorfní.
Teď jen doufám, že jsem nikde neudělal hloupou chybu. Důkaz je to o dost komplikovanější než ten chybný z odpoledne :-).
Offline
#53 20. 11. 2011 18:05 — Editoval check_drummer (20. 11. 2011 18:05)
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Další izomorfní algebry
↑ Pavel Brožek:
Ahoj. Bohužel jsem včera z časových důvodů nestíhal sledovat toto vlákno - a jestli to chápu dobře, tak úloha by měla být vyřešena. Můžeš mi prosím poslat odkaz na příspěvek v tomto vláknu, který charakterizuje ekvivalentní podmínku, kdy jsou struktury mN a nN ekvivalentní? Děkuji.
"Máte úhel beta." "No to nemám."
Offline
#54 20. 11. 2011 18:47 — Editoval Pavel Brožek (20. 11. 2011 18:48)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ check_drummer:
Ahoj, ano, pokud jsem se nikde nezmýlil, tak je to vyřešené (ale možná má smysl hledat jednodušší řešení, protože to moje je poměrně zdlouhavé). ↑↑ Tady: je popsané, kdy jsou algebry isomofrní. Ukázalo se, že v ostatních případech algebry isomorfní nejsou.
Offline
#55 21. 11. 2011 08:12 — Editoval Andrejka3 (21. 11. 2011 19:59)
Re: Další izomorfní algebry
Ahoj.
Zatím jsem vás nedohonila ve vašich důkazech a myšlenkách, ještě jsem na to od té doby neměla klid. Takže to, co dále budu psát bude asi nadbytečné. Úloha je již vyřešená a pochybuju, že to jsou nové objevy. Možná to později editem odstraním.
Kde je odlišnost struktury 2N a 4N? Už jsme na to narazili předtím. 4^3 = 8^2, coz je zajimave. Kdybychom hledali izomorfismus z 4N do 2N, tak musime priradit ctyrce cislo, ktere neni delitelne 4 a zaroven jeho treti mocnina se da napsat jako druha mocnina nejakeho cisla z 2N, neboli priradit takove cislo 2n, kde 2 nedeli n, ze  je z 2N. Takove ale neni.
je z 2N. Takove ale neni.  je iracionalni. Pamatuju si, ze nam ctyrka a osmicka delaly problemy.
je iracionalni. Pamatuju si, ze nam ctyrka a osmicka delaly problemy.
EDIT:
PRIPOMINKA
Buď  nerostoucí psl.,
nerostoucí psl., 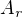 prislusna algebra.
prislusna algebra.  jako v Tvrzeni 1.
jako v Tvrzeni 1.
Tvrdí se, že jediný prvek  algebry
algebry 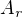 , ktery splnuje rovnost
, ktery splnuje rovnost 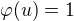 je
je 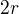 . To neni pravda. Pokud "delka" posloupnosti
. To neni pravda. Pokud "delka" posloupnosti  (pocet nenulovych clenu) je
(pocet nenulovych clenu) je  , posloupnost
, posloupnost 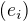 je nulova vsude az na i-te misto, kde ma jednicku, pak
je nulova vsude az na i-te misto, kde ma jednicku, pak 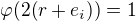 , je-li
, je-li  a
a  . Nebo nechapu text za Tvrzenim 1.
. Nebo nechapu text za Tvrzenim 1.
edit: Výše není pravda. Omyl.
EDIT:
Navržené značení a ideje usnadní důkaz toho, že 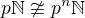 , kde
, kde  je prvocislo a
je prvocislo a  :
:
Dalsim krokem by bylo ukazat, ze
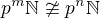 , kdyz
, kdyz 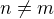 .
.Zajimava cast je i tato.
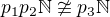 pro tri ruzna prvocisla.
pro tri ruzna prvocisla.Tyto myšlenky (tak trochu přejaté z předchozího důkazu) možná lze nějak zobecnit. Problém dělá bohužel to, že relace "nebýt izomorfní" není transitivní...
Edit: Odstraněno podezření z neplatnosti důkazu.
Edit: Přidána část pro p^m, p^n.
What does a drowning number theorist say?
'log log log log ...'
Offline
#56 21. 11. 2011 15:06 — Editoval Andrejka3 (21. 11. 2011 18:28)
Re: Další izomorfní algebry
Takže to vypadá, že ten důkaz bohužel padá ne? I kdyby ano, mohou být užitečné jeho mezivýsledky.
Edit: Nesmysl. Tento příspěvek je chybný.
What does a drowning number theorist say?
'log log log log ...'
Offline
#57 21. 11. 2011 18:22
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
Ahoj,
Andrejka3 napsal(a):
EDIT:
PRIPOMINKA
Buďnerostoucí psl.,
prislusna algebra.
jako v Tvrzeni 1.
Tvrdí se, že jediný prvekalgebry
, ktery splnuje rovnost
je
. To neni pravda. Pokud "delka" posloupnosti
(pocet nenulovych clenu) je
, posloupnost
je nulova vsude az na i-te misto, kde ma jednicku, pak
, je-li
a
. Nebo nechapu text za Tvrzenim 1.
Prvek 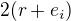 se dá podle mě rozložit třemi způsoby:
se dá podle mě rozložit třemi způsoby:
takže 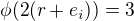 . Nebo mi něco uniká?
. Nebo mi něco uniká?
Dále jsem tvůj příspěvek nečetl, tak se ke zbytku vyjádřím ještě později.
Offline
#58 21. 11. 2011 18:25 — Editoval Andrejka3 (21. 11. 2011 18:27)
Re: Další izomorfní algebry
↑ Pavel Brožek:
Děkuji.
Dám pryč mystifikující přídavná jména kolem Tvého důkazu.
What does a drowning number theorist say?
'log log log log ...'
Offline
#59 21. 11. 2011 18:43
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
Co prosím znamená značení 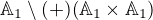 ? Nikdy jsem se s ním asi nesetkal a z kontextu mi to není jasné.
? Nikdy jsem se s ním asi nesetkal a z kontextu mi to není jasné.
Offline
#60 21. 11. 2011 18:46
Re: Další izomorfní algebry
↑ Pavel Brožek:
Množinový rozdíl dvou množin. První je nosič algebry. Druhou množinou je obraz binární operace + všech dvojic všech prvků z nosiče algebry, "image +"
Písmo by nemělo být dvojité, protože se jedná o nosiče algeber - množiny a ne algebry.
What does a drowning number theorist say?
'log log log log ...'
Offline
#61 21. 11. 2011 19:06
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
Díky, už rozumím. Prošel jsem si už celý ↑ příspěvek: a zdá se mi, že je tam vše v pořádku :-).
Offline
#62 21. 11. 2011 19:44
Re: Další izomorfní algebry
↑ Pavel Brožek:
Casem mozna neco dodam do prispevku vyse, kde jsem psala nejake specialni situace.
What does a drowning number theorist say?
'log log log log ...'
Offline
#63 21. 11. 2011 20:24
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Další izomorfní algebry
Dnes jsem o tom přemýšlel a pokud jsou mé následující úvahy správné, je situace velmi jednoduchá - až se skoro divím. :-) Takže budu rád, když najdete v těch úvahách nějaký problém. :-)
Tedy - myšlenka je následující (všechny algebry jsou s "klasickou" operací násobení): mějme izomorfismus f z 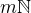 na
na 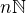 . Sestrojíme izomorfismus g z
. Sestrojíme izomorfismus g z 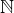 na
na 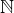 . Tímto izomorfismem je
. Tímto izomorfismem je 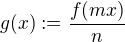 (což se snadno ověří).
(což se snadno ověří).
O f lze odvodit, že platí f(m)=n a z toho plyne, že  a tedy
a tedy 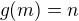 (1).
(1).
Ovšem všechny izomorfismy h z 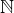 na
na 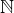 splňují:
splňují:
a) h(1)=1
b) 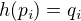 , kde
, kde  a
a 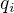 jsou prvočísla (pro různá i různá)
jsou prvočísla (pro různá i různá)
c) tedy pro 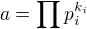 je
je 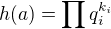
Z bodu c) a bodu (1) už hned plyne, že je-li m tvaru 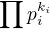 , je n tvaru
, je n tvaru  , což jsme chtěli ukázat.
, což jsme chtěli ukázat.
"Máte úhel beta." "No to nemám."
Offline
#64 21. 11. 2011 20:36
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Další izomorfní algebry
Andrejka3 napsal(a):
4^3 = 8^2, coz je zajimave. Kdybychom hledali izomorfismus z 4N do 2N, tak musime priradit ctyrce cislo, ktere neni delitelne 4 a zaroven jeho treti mocnina se da napsat jako druha mocnina nejakeho cisla z 2N, neboli priradit takove cislo 2n, kde 2 nedeli n, ze
je z 2N. Takove ale neni.
je iracionalni. Pamatuju si, ze nam ctyrka a osmicka delaly problemy.
Ahoj, asi už mi to nemyslí - proč číslo přiřazené čtyřce není dělitelné 4?
A proč jeho třetí mocninu lze napsat jako druhou mocninu nějakého čísla z 2N?
Děkuji.
Já myslím, že musí platit f(4)=2 - nebo ne? Obecně f(m)=n...
"Máte úhel beta." "No to nemám."
Offline
#65 21. 11. 2011 20:39
Re: Další izomorfní algebry
↑ check_drummer:
Overuji homomorfismus: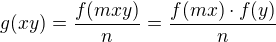 a zde je problem. Co kdyz
a zde je problem. Co kdyz  ?
?
What does a drowning number theorist say?
'log log log log ...'
Offline
#66 21. 11. 2011 20:48 — Editoval Andrejka3 (21. 11. 2011 21:02)
Re: Další izomorfní algebry
↑ check_drummer:
Mame izomorfismus  . Je-li
. Je-li  , pak
, pak 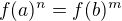
proč číslo přiřazené čtyřce není dělitelné 4?
Protoze kdyby bylo, pak lze napsat jako 2*2*a. Pak by diky inverznimu izomorfismu bylo 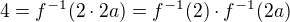 , tedy existuji dva prvky z 4N takove, ze jejich soucin je 4. Ale to neni mozne, protoze oba cinitele jsou z 4N, tedy jejich soucin je aspon 16.
, tedy existuji dva prvky z 4N takove, ze jejich soucin je 4. Ale to neni mozne, protoze oba cinitele jsou z 4N, tedy jejich soucin je aspon 16.
Já myslím, že musí platit f(4)=2 - nebo ne? Obecně f(m)=n...
Ano, ale tehdy mi to jeste nedoslo. Vlastne diky poznamce za Tvrzeni 1 na str 3 to plati.
What does a drowning number theorist say?
'log log log log ...'
Offline
#67 21. 11. 2011 20:50
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
Pokud y není dělitelné m, tak nemůžeš psát 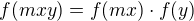 . Vztah
. Vztah 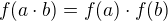 požadujeme jen pro
požadujeme jen pro  z dané algebry.
z dané algebry.
↑ check_drummer:
Přiznám se, že se mi také nedaří snadno ověřit, že 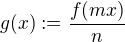 je homomorfismus.
je homomorfismus.
Offline
#68 21. 11. 2011 21:00 — Editoval Andrejka3 (21. 11. 2011 21:06)
Re: Další izomorfní algebry
↑ Pavel Brožek:
Bohuzel. Dabelsky napad to byl, ale homomorfismus to nemuze.
Edit: Ach jo, radeji zpomalim.
Neumim overit, ze to je homomorfismus.
What does a drowning number theorist say?
'log log log log ...'
Offline
#69 21. 11. 2011 21:05
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
Proč to nemůže být homomorfismus?
Offline
#70 21. 11. 2011 21:13
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Další izomorfní algebry
↑ Pavel Brožek:
Předpokládám, že f(m)=n, což jsem si myslel, že musí platit, ale teď mě bohužel nenapadá argument, proč. Ale pokud to platí, tak máme:
f(m.a.m.b)/n^2=f(m).f(m.a.b)/n^2=f(m.a.b)/n=g(a.b)
a také
f(m.a.m.b)/n^2=f(ma)/n.f(mb)/n=g(a).g(b).
tj. g(a.b)=g(a).g(b)
"Máte úhel beta." "No to nemám."
Offline
#71 21. 11. 2011 21:25 — Editoval Andrejka3 (21. 11. 2011 21:34)
Re: Další izomorfní algebry
↑ check_drummer:
Tak doufám že se nepletu. Všechno jsem zapsala a chybu tam žádnou nevidím.
Smekám!
EDIT:
Skutečně, kolega už ukázal, že  ve svem dukazu na str 3 v textu za Tvrzeni 1.
ve svem dukazu na str 3 v textu za Tvrzeni 1.
V algebre mN je 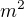 jediny prvek, ktery lze zapsat jako soucin dvou cisel z algebry prave jednim zpusobem a to
jediny prvek, ktery lze zapsat jako soucin dvou cisel z algebry prave jednim zpusobem a to 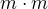 . Diky teto vyjimecnosti se musi na sebe tyto prvky zobrazovat.
. Diky teto vyjimecnosti se musi na sebe tyto prvky zobrazovat.
What does a drowning number theorist say?
'log log log log ...'
Offline
#72 21. 11. 2011 21:37 — Editoval Pavel Brožek (21. 11. 2011 21:42)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ check_drummer:
Opravdu nádherné. Tvůj důkaz vlastně dává i jednoduchý návod, jak isomorfismus sestrojit, když to jde – stačí obrátit vztah 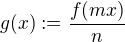 na
na  , g už si pak můžeme snadno zvolit.
, g už si pak můžeme snadno zvolit.
Offline
#74 21. 11. 2011 21:48
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
Já také děkuji, tohle téma mě opravdu bavilo – tolik zvratů při řešení tak jednoduše zadaného problému… :-)
Offline
#75 22. 11. 2011 18:17
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Další izomorfní algebry
Také děkuji za spolupráci při řešení tohoto velmi zajímavého problému - myslím, že by si tohle téma zasloužilo přesun do Zajímavých aspoň in memoriam. :-)
Jinak jsem se ještě zamyslel nad tím, proč f(m)=n. Tak to schválně napíšu a pak se podívám. :-)
Nechť je f(m)=i.n a f(j.m)=n pro nějaká i,j. Pak je:
n.n=f(j.m).f(j.m)=f(j.m.j.m)=f(m.m.j.j)=f(m).f(m.j.j)=i.n.f(m.j.j).
Tj. porovnáme členy zcela vlevo a vpravo:
n/i=f(m.j.j). Ovšem n je nejmenší hodnota funkce f, tedy musí být i=1, tedy
f(m.j.j)=n. Ovšem j je prostá - a je i f(m.j)=n a tedy musí platit m.j=m.j.j, tj. j=1.
Celkem tedy máme:
f(m)=n (ten poslední krok s j jsme si vlastně už mohli odpustit)
"Máte úhel beta." "No to nemám."
Offline
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Další izomorfní algebry (TOTO TÉMA JE VYŘEŠENÉ)
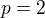 . Oznacme sproste prislusne algebry
. Oznacme sproste prislusne algebry 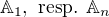 . Plati v
. Plati v 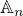
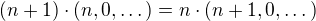
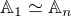 , pak musi v
, pak musi v 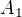 existovat dvojice prvku
existovat dvojice prvku 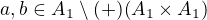 takova, ze
takova, ze 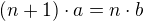 . Protoze ale
. Protoze ale 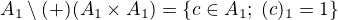 staci psat rovnici pro prvni slozku
staci psat rovnici pro prvni slozku , aby bylo zrejme, ze takova dvojice neexistuje a algebry maji jine struktury.
, aby bylo zrejme, ze takova dvojice neexistuje a algebry maji jine struktury. . BUNO at
. BUNO at 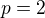 .
.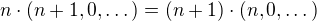 . Diky poznamce za Tvrzenim 1 vime, ze pokud existuje izomorfismus nasich dvou algeber, je obraz prvku
. Diky poznamce za Tvrzenim 1 vime, ze pokud existuje izomorfismus nasich dvou algeber, je obraz prvku  roven
roven  .
. musi existovat prvek
musi existovat prvek 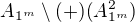 tak, ze
tak, ze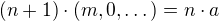 , tj. existuje
, tj. existuje 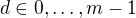 takove, ze
takove, ze  . Odtud vidime:
. Odtud vidime:
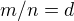 , coz je spor s definici
, coz je spor s definici  , tedy algebry nejsou isomorfni.
, tedy algebry nejsou isomorfni. 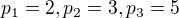 . Oznacme indukovane izomorfismy do prislusnych algeber posloupnosti
. Oznacme indukovane izomorfismy do prislusnych algeber posloupnosti  , resp.
, resp. 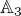 . V alg.
. V alg. 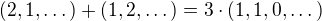 . Kdyby
. Kdyby 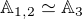 , pak existuje trojice prvku
, pak existuje trojice prvku 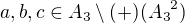 takova, ze
takova, ze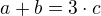 . Jakmile napiseme rovnici pro treti clen posloupnosti, vyjde najevo, ze takova trojice neexistuje:
. Jakmile napiseme rovnici pro treti clen posloupnosti, vyjde najevo, ze takova trojice neexistuje: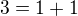 a algebry nejsou izomorfni.
a algebry nejsou izomorfni.