Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 20. 08. 2008 09:52 — Editoval musixx (20. 08. 2008 09:58)
Re: Rovnice
Asi by to chtelo si uvedomit, jaky je obecny navod na reseni rovnic a nerovnic s absolutni hodnotou. Najdeme tzv. nulove body, tedy body, kde je argument absolutni hodnoty nulovy. Tyto nulove body nam rozdeli realnou osu na nekolik intervalu a reseni hledame vzdy v kazdem z techto intervalu. Resenim rovnice je cislo, resenim nerovnice je interval. U rovnice overime, je-li vysledek v intervalu, ve kterem jsme pocitali. Je-li tak, pak jsme nalezli reseni, neni-li tak, pak reseni v tomto intervalu neexistuje. U nerovnice je vysledkem prunik intervalu, ve kterem jsme pocitali, s intervalem, ktery nam vysel jako reseni.
Poznamka: je celkem jedno, ke kteremu intervalu "pridelime" onen nulovy bod, nebot 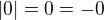 .
.
Aplikuji-li tedy tuto obecnou metodu na  , mam:
, mam:
Nulovy bod je jediny, a to  .
.
I. Na intervalu 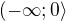 je tedy
je tedy  totez jako
totez jako  . Tedy mame resit
. Tedy mame resit  , coz dava
, coz dava  , tedy
, tedy  , tedy resenim by byl interval
, tedy resenim by byl interval 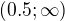 . My jsme se ale zajimali jen o ta
. My jsme se ale zajimali jen o ta  , ktera jsou mensi nez nula, neboli tento prvni interval nam nedal zadne reseni.
, ktera jsou mensi nez nula, neboli tento prvni interval nam nedal zadne reseni.
II. Na intervalu 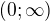 je
je  totez jako
totez jako  . Tedy mame resit
. Tedy mame resit  , coz dava
, coz dava  , coz nema reseni, neboli resenim je prazdny interval a ten v pruniku s cimkoli dava prazdny interval.
, coz nema reseni, neboli resenim je prazdny interval a ten v pruniku s cimkoli dava prazdny interval.
Proto prvni uloha nema reseni.
Uloha druha ma nulovy bod 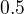 .
.
I. Na intervalu 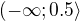 je tedy
je tedy 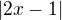 totez jako
totez jako 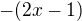 . Tedy mame resit
. Tedy mame resit  , coz dava
, coz dava  , tedy
, tedy  , tedy resenim je interval
, tedy resenim je interval 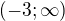 v pruniku s
v pruniku s 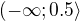 , tedy
, tedy 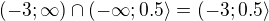 .
.
II. Na intervalu 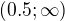 je
je 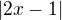 totez jako
totez jako 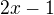 . Tedy mame resit
. Tedy mame resit  , coz dava
, coz dava  , tedy resenim je interval
, tedy resenim je interval 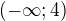 v pruniku s
v pruniku s 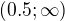 , tedy
, tedy 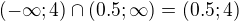 .
.
Celkove ma tedy druha uloha reseni 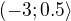 a
a 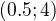 , tedy sjednoceni techto dvou intervalu
, tedy sjednoceni techto dvou intervalu 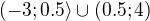 , coz samozrejme je
, coz samozrejme je 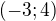 .
.
Toliko k obecnemu reseni.
------------------------------------------------------------------------------
V takovychto jednoduchych pripadech je vsak take mozno udelat snazsi uvahu. Neni na ni vsak zadny "mustr" a rekl bych, ze vyzaduje jistou zkusenost.
Nerovnost prikladu prvniho je zrejme splnena jen tehdy, je-li leva strana kladna (vzdyt absolutni hodnota je vzdy nezaporna a chceme, aby to vlevo bylo vetsi). Leva strana je ale kladna jen pro  kladne (a to jeste ani dokonce ne pro vsechna), no ale nikdy preci nemuze byt
kladne (a to jeste ani dokonce ne pro vsechna), no ale nikdy preci nemuze byt 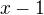 vetsi nez
vetsi nez  . Proto zadne reseni.
. Proto zadne reseni.
Nerovnost prikladu druheho je nerovnosti mezi nezapornymi cisly, tedy umocneni na druhou je ekvivalentni uprava, a tedy resime  , coz po odecteni a vydeleni ctymi dava
, coz po odecteni a vydeleni ctymi dava  . Rozkladem na korenove cinitele mame
. Rozkladem na korenove cinitele mame  , no a soucin dvou cinitelu je zaporny jen tehdy, je-li jeden cinitel zaporny a druhy kladny. Kdyz je ale
, no a soucin dvou cinitelu je zaporny jen tehdy, je-li jeden cinitel zaporny a druhy kladny. Kdyz je ale 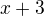 zaporne, tak
zaporne, tak 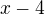 nebude urcite kladne (vzdyt je mensi nez
nebude urcite kladne (vzdyt je mensi nez 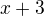 ). Zbyva tedy
). Zbyva tedy  a soucasne
a soucasne  , coz dava presne
, coz dava presne 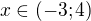 .
.
Offline
