Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#7 20. 08. 2008 09:22 — Editoval Marian (20. 08. 2008 09:23)
Re: Podmnožiny
↑ joker:↑ ttopi:
Skutečně tam patří i prázdná množina, nebo? je jistě splněna inkluze 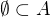 , kde
, kde  je libovolná množina. Navíc platí, že počet všech podmnožin libovolné množiny
je libovolná množina. Navíc platí, že počet všech podmnožin libovolné množiny  je roven
je roven 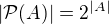 , kde
, kde 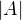 značí mohutnost množiny
značí mohutnost množiny  , tedy počet (různých) prvků a
, tedy počet (různých) prvků a  je potenční množina množiny
je potenční množina množiny  . Odtud počet všech podmnožin množiny
. Odtud počet všech podmnožin množiny 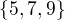 je roven
je roven  .
.
Offline
#8 20. 08. 2008 10:13 — Editoval musixx (20. 08. 2008 10:16)
Re: Podmnožiny
↑ Marian: A pro nekonecnou  by se asi sluselo dodat, ze symbolem
by se asi sluselo dodat, ze symbolem 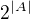 prestavame rozumet pocetni operaci, ale rozumime tim mnozinu vsech zobrazeni z
prestavame rozumet pocetni operaci, ale rozumime tim mnozinu vsech zobrazeni z  do (ne na!)
do (ne na!)  (ztotoznujeme totiz
(ztotoznujeme totiz  s libovolnou dvouprvkovou mnozinou, resp. se odvolavame na axiomy teorie mnozin a
s libovolnou dvouprvkovou mnozinou, resp. se odvolavame na axiomy teorie mnozin a  bereme jen jako symbol pro
bereme jen jako symbol pro 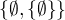 - no a pri tomto ztotozneni je vlastne take jedno, jestli mluvime o
- no a pri tomto ztotozneni je vlastne take jedno, jestli mluvime o  nebo
nebo 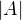 , abych byl uz teda uplne korektni).
, abych byl uz teda uplne korektni).
Je vsak samozrejme pravda, ze ve svete konecnych mnozin nejde o nic vic nez o umocneni dvojky na pocet prvku one mnoziny.
Offline
