Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Rekurentní rovnice - mistrovská metoda
#1 27. 11. 2011 18:24 — Editoval mr.rubik (27. 11. 2011 19:58)
Rekurentní rovnice - mistrovská metoda
Zdravím všechny přítomné,
za domácí úkol jsem dostal vyřešit rekurentní rovnici (diskrétní matematika). Byl bych vděčný za pomoc.
Funkce t(n), rekurentně: 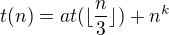
Úkolem je pomocí mistrovské metody nalézt těsnou asymptotickou mez t(n)  pro všechny hodnoty parametrů.
pro všechny hodnoty parametrů.
parametry zde

V mistrovské metodě jsou tři možnosti (v rychlosti je tu připomenu)
a) pokud  pak
pak 
b) pokud  pak
pak 
c) pokud  ... pak
... pak 
Já jsem začal řešit a) takto: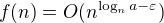
 - p jsem si určil sám pro sebe pro přehlednost
- p jsem si určil sám pro sebe pro přehlednost
a protože v logaritmu nesmí být p <= 0, tak jsem řešil jen pro p > 0 a tedy: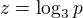 z jsem si taky určil sám
z jsem si taky určil sám
z musí být menší než nula, protože b je z intervalu (0,1), to z toho plyne (doufám :) )
dále tedy: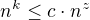
Došel jsem až sem a teď nevím, jak určit konkrétní hodnoty parametrů tak, aby to platilo. Respektive udělal jsem několik pokusů, ale opravdu nevím. Dost jsem se ve složitostech ztrácel.
Další části mistrovské metody budou - předpokládám - analogické. Prosil bych tedy o kontrolu dosavadního postupu a o radu, co dál.
EDIT: jedná se sice o diskrétní matematiku, ale ne na VŠB, tak jsem téma umístil sem, doufám, že je to tak správně
Díky, MrRubik
Offline
#3 28. 11. 2011 22:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rekurentní rovnice - mistrovská metoda
↑ mr.rubik:
Zdravím, bude to čistě Moderatorská osvěta (mistrovskou metodu jsem sice teď přečetla z materiálů, ale diskrétní matematika je zapovězena, mé mistrovství končí u trojčlenky), tak jen:
tečka značí, že jsi do tématu přispíval, téma jsi vytvořil správně, v sekci DIM VŠB se objevují také úlohy z jiných škol, snad nebude námitka, pokud přesunu a budeš více viditelný, případně vážený Moderátor pan Petr Kovář přesune jinam (děkuji).
Je to asi všechno, co mohu udělat - pokud se podíváš na stav odpovězených témat v sekci VŠ, řekla bych, že je období odevzdávání nějakých práci (alespoň v mém okolí to tak je). Ať se podaří.
Offline
#5 28. 11. 2011 22:55 — Editoval FailED (28. 11. 2011 23:01)
Re: Rekurentní rovnice - mistrovská metoda
↑ mr.rubik:
Zdravím,
ten překlad zní opravdu hrozně :)
Dost jsem se ve složitostech ztrácel.
Bez toho to opravdu nepůjde.
Protože pro n>0 je n^k>0, můžeme to převést na  , z toho už k vyjádříš ne?
, z toho už k vyjádříš ne?
Offline
#8 30. 11. 2011 00:17
Re: Rekurentní rovnice - mistrovská metoda
↑ mr.rubik:
master theorem -> mistrovská metoda
↑ Dworzaaa:
Co v čem nevidíš? Ta limita je jen přepsání definice, 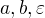 jsou konstanty takže vyjde kladně právě když
jsou konstanty takže vyjde kladně právě když  .
.
Offline
#10 30. 11. 2011 12:09 Příspěvek uživatele theCAESAR byl skryt uživatelem theCAESAR.
#12 30. 11. 2011 15:46
Re: Rekurentní rovnice - mistrovská metoda
↑ theCAESAR:
tohle reseni vypada rozumne... projevi se na vysledku nejak ta dolni cela cast v 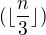 ? Nevim, kde by se to mohlo projevit, ale zase se mi nezda, ze bych ji moh uplne zahodit..
? Nevim, kde by se to mohlo projevit, ale zase se mi nezda, ze bych ji moh uplne zahodit..
Offline
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Rekurentní rovnice - mistrovská metoda

 kde a je
kde a je  protože ten logaritmus je vždycky záporný a
protože ten logaritmus je vždycky záporný a  a
a 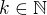 Tzn že neplatí ani
Tzn že neplatí ani 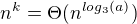 pak platí třetí možnost a to že
pak platí třetí možnost a to že 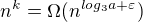 a také platí
a také platí 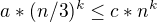
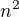 připočítával konstantu
připočítával konstantu  stejně ti z toho nikdy nevyjde že
stejně ti z toho nikdy nevyjde že 