Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nejmenší generátor svazu ekvivalencí konečné množiny (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 12. 2011 19:40 — Editoval Andrejka3 (01. 12. 2011 20:50)
Nejmenší generátor svazu ekvivalencí konečné množiny
Ahoj, prosím o nápovědu pro následující úlohu.
Zadání:
Buď  konečná množina. Najděte nejmenší množinu generátorů svazu
konečná množina. Najděte nejmenší množinu generátorů svazu  .
.
Pojmy a značení
Co jsem zatím zjistila
Výsledek podle skript
Edit: Co je svaz
Edit: souvislost svazu a svazove usp. mnoziny, nas priklad.
Co jsem zatím zjistila.
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 01. 12. 2011 20:15
- check_drummer

- Příspěvky: 4905
- Reputace: 105
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ Andrejka3:
Ahoj, jak jsou pro tento konkétní svaz definovány operace 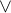 a
a 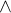 ?
?
"Máte úhel beta." "No to nemám."
Offline
#3 01. 12. 2011 20:20 — Editoval Andrejka3 (01. 12. 2011 20:20)
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ check_drummer:
Ahoj, právě jsem dopsala jak to je, je to v pojmech a označeních v úvodní zprávě.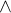 odpovida pruniku.
odpovida pruniku. 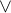 odpovida skoro sjednoceni - tady se ale musi dat pozor, aby relace kterou dostanem, byla opet ekvivalence, takze to je podle mě prunik vsech ekvivalenci, ktere obsahuji ty dve ekvivalence. Tedy nejmenší ekvivalence, která obsahuje jejich sjednocení. Pokusím se to zapsat pomocí texu, ale potřebuju tam dva řádky pod průnikem a to jsem ještě nedělala :)
odpovida skoro sjednoceni - tady se ale musi dat pozor, aby relace kterou dostanem, byla opet ekvivalence, takze to je podle mě prunik vsech ekvivalenci, ktere obsahuji ty dve ekvivalence. Tedy nejmenší ekvivalence, která obsahuje jejich sjednocení. Pokusím se to zapsat pomocí texu, ale potřebuju tam dva řádky pod průnikem a to jsem ještě nedělala :)
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 01. 12. 2011 20:43
- check_drummer

- Příspěvky: 4905
- Reputace: 105
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ Andrejka3:
Takže 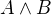 je největší ekvivalence obsahující každý prvek z A a B (tj. průnik) a
je největší ekvivalence obsahující každý prvek z A a B (tj. průnik) a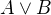 je nejmenší ekvivalence obsahující aspoň jeden prvek z A a B (takový hybrid "sjednocení a uzavřenosti")?
je nejmenší ekvivalence obsahující aspoň jeden prvek z A a B (takový hybrid "sjednocení a uzavřenosti")?
"Máte úhel beta." "No to nemám."
Offline
#5 01. 12. 2011 20:48 — Editoval Andrejka3 (01. 12. 2011 20:56)
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ check_drummer:
Ano, neboli infimum a supremum. Největší dolní závora a nejmenší horní závora. Za chvíli to zapíšu líp díky kamarádovi kolegovi, který mi poradil :P
Kdybychom se pohybovali v množině všech podmnožin například, tak by odpovídající operace pro 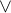 bylo obycejne sjednoceni. Tady musime dat pozor, aby to byla ekvivalence - sjednoceni dvou ekvivalenci obecne neni ekvivalence.
bylo obycejne sjednoceni. Tady musime dat pozor, aby to byla ekvivalence - sjednoceni dvou ekvivalenci obecne neni ekvivalence.
Edit: k tomu hybridu ne.
To 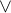 odpovida nejmensi ekvivalenci, ktera obsahuje obe, ktere davame do operatoru.
odpovida nejmensi ekvivalenci, ktera obsahuje obe, ktere davame do operatoru.
viz ted opravena prvni zprava, jeste to tu zkopiruji editem.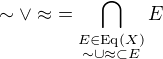
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 01. 12. 2011 21:05
- check_drummer

- Příspěvky: 4905
- Reputace: 105
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ Andrejka3:
Tak co třeba na 3prvkové nebo 4prvkové množině - jak budou takové generátory vypadat?
"Máte úhel beta." "No to nemám."
Offline
#7 01. 12. 2011 21:17 — Editoval Andrejka3 (02. 12. 2011 13:58)
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ check_drummer:
Triprvkova: 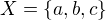
Znacme pro jednoduchost jen "nediagonalni" prvky ekvivalenci (reflexivita) a doplnme na symetrickou relaci.
Pak {(a,b)} {(a,c)} {(b,c)} jiste generuje svaz ekvivalenci na triprvkove mnozine. Je totiz  a
a 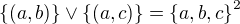 .
.
Ctyrprvkova 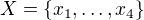
Generatory jsou 
Zkoušela jsem si nakreslit Hasse diagram pro čtyřprvkovou množinu - byl to odporný obrázek. Ve třetím patře z některých jdou dolů tři nožičky a z jiných dvě. Asi mi něco podstatného uniká. Nechápu, jak dojít k tomu výsledku. Taky zrovna nejsem doma v diskrétní matematice a kombinatorice zvláště :)
Edit: a jestli je výsledek správně, tak nemůžu určitě vybírat jen z jednoho "patra", musím vybrat nějaké, které nejsou porovnatelné, tj. ani jedna není podmnožinou druhé, aspoň si to myslím.
Možná z toho nejtlustšího patra - jestli si rozumíme, co tím myslím - moc teda nevím jak jinak to popsat.
Akorát třeba v té čtyřprvkové je dohromady asi 5 pater? třetí to nejmohutnější - už si nevybavuji kolik jsem tam měla bodů...
Edit: nekonzistence. Místo množiny X jsem měla množinu A.
What does a drowning number theorist say?
'log log log log ...'
Offline
#8 02. 12. 2011 13:09 — Editoval Andrejka3 (02. 12. 2011 19:55)
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
Ahoj, mám návrh.
Kreslila jsem si svaz ekvivalencí čtyřprvkové množiny.Vyšel z toho takový hezký čtyřpatrový diamant se špičkou nahoře a dole.
Mějme  . Existuje {oprava: 15}14 ekvivalencí takové množiny, z nichž dvě bych nazvala nevlastní. Budu je znázorňovat maticemi sousednosti, přičemž budu psát jen netriviální členy - ty, které jsou nad hlavní diagonálou.
. Existuje {oprava: 15}14 ekvivalencí takové množiny, z nichž dvě bych nazvala nevlastní. Budu je znázorňovat maticemi sousednosti, přičemž budu psát jen netriviální členy - ty, které jsou nad hlavní diagonálou.
Každé ekvivalenci jsem přiřadila nějaké číslo. Podstatné nebudou ale ekvivalence
 a
a  . Úkolem je teď najít z 13 ekvivalencí 1 až 13 čtveřici takovou, která generuje celý svaz. Přitom víme, že 2. i 3. patra obě zvlášť generují celý svaz. Jak vypadají cesty v Hasse diagramu? Budu psát cesty z druhého do třetího patra:
. Úkolem je teď najít z 13 ekvivalencí 1 až 13 čtveřici takovou, která generuje celý svaz. Přitom víme, že 2. i 3. patra obě zvlášť generují celý svaz. Jak vypadají cesty v Hasse diagramu? Budu psát cesty z druhého do třetího patra:Bohužel existuje {oprava: 13}12 nad 4 výběrů, což je {oprava:?}495 a to je na člověka příliš (i když pár jsem jich udělala, a jezdit po cestičkách mě bavilo) :) . Z těch 495 očekávám, že nebudou všechny "nezávislé", očekávám nějakou symetrii při převrácení diagramu vzhůru nohama{to se zvlast nepotvrzuje}. Pokud by se našel náhodou někdo, koho by bavilo zkusit udělat program a brute force zjistit, jestli taková čtveřice existuje, bylo by to skvělé. Svůj PC budu mít k dispozici až večer, kromě toho programovat moc neumím.
Mám rovněž podezření, že ten nabízený výsledek je špatný. Ještě se uvidí...
Edit: problémy s TeXem.
Nekonzistence. Místo množiny X psáno množina A.
Edit: doplneni chybejici ekvivalence
What does a drowning number theorist say?
'log log log log ...'
Offline
#9 02. 12. 2011 13:39
- check_drummer

- Příspěvky: 4905
- Reputace: 105
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ Andrejka3:
První skytý text ukazuje samé LaTexové chyby...
Mně to přijde velmi zajímavé, že stačí pouze 4 ekvivalence...
Řekl bych, že všechny 4 budou neporovnatelné (to by byly příliš závislé), ale je to jen tip.
Jak definuješ patra? V k-tém patře jsou ty prvky, do nichž se lze dostat z prvku 0 (identita) cestou délky k a žádou kratší?
Může pro dostatčně velký počet prvků množiny X (i když pak ji nazýváš A) být počet pater větší než (libovolné) číslo K?
Může pro dostatčně velký počet prvků množiny X (i když pak ji nazýváš A) být počet prvků v nějakém (eventuelně každém kromě prvního a posledního) patře větší než (libovolné) číslo L?
Bohužel nemám teď čas, abych si to naprogramoval, mohlo by to ale dost pomoci. Otázkaje, pro jak velkou X by hrubé síle trval výpočet neúnosně dlouho...
"Máte úhel beta." "No to nemám."
Offline
#10 02. 12. 2011 13:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ Andrejka3:
Zdravím, opravila jsem 1. zápis v hide - může tak být? Případně se ozv v některém tématu ohledně TeX v sekci připomínek nabo na pískovišti. Ať se vede.
Offline
#12 02. 12. 2011 13:53 — Editoval Andrejka3 (02. 12. 2011 13:56)
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ check_drummer:
Ano, tak definuji patra, jak píšeš. Musím se ještě dodatečně ujistit, že neexistují žádné cesty mezi prvky v jednom patře, tj. že prvky ze stejného patra jsou neporovnatelné. Nevím, jestli to bude stejně i u množin vyšší mohutnosti.
Může pro dostatčně velký počet prvků množiny X (i když pak ji nazýváš A) být počet pater větší než (libovolné) číslo K?
Může pro dostatčně velký počet prvků množiny X (i když pak ji nazýváš A) být počet prvků v nějakém (eventuelně každém kromě prvního a posledního) patře větší než (libovolné) číslo L?
Ano, to jsou zajímavé otázky.
Edit: Každopádně, kdybychom žádný čtyřprvkový generátor pro svaz ekvivalencí čtyřprvkové množiny nenašli ani brute force... :P
Edit: V případě 4 - prvkové jistě jsou v patrech neporovnatelné ekvivalence.
What does a drowning number theorist say?
'log log log log ...'
Offline
#13 02. 12. 2011 15:23 — Editoval Andrejka3 (02. 12. 2011 15:26)
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
Může pro dostatčně velký počet prvků množiny X (i když pak ji nazýváš A) být počet prvků v nějakém (eventuelně každém kromě prvního a posledního) patře větší než (libovolné) číslo L?
Ano, například v druhém patře je právě  ekvivalencí.
ekvivalencí.
Může pro dostatčně velký počet prvků množiny X (i když pak ji nazýváš A) být počet pater větší než (libovolné) číslo K?
Vypadá to, že ano. Zatím pro 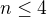 je počet pater roven mohutnosti množiny
je počet pater roven mohutnosti množiny  .
.
Každopádně existuje cesta z nevlastní do nevlastní ekvivalence takováto: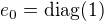
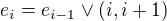 , kde
, kde  , takže to je přes
, takže to je přes  cestiček.
cestiček. 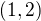 rozumím ekvivalenci, kdy
rozumím ekvivalenci, kdy 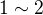 , neboli maticove, nad horni diagonalou je jednicka na miste radek 1, sloupec 2 a jinde nad diagonálou jsou nuly.
, neboli maticove, nad horni diagonalou je jednicka na miste radek 1, sloupec 2 a jinde nad diagonálou jsou nuly.
Nevím, zda neexistuje kratší cesta mezi těmito ekvivalencemi.
What does a drowning number theorist say?
'log log log log ...'
Offline
#15 02. 12. 2011 15:45
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ radekm:
Upřímně řečeno nevím. Myslela jsem si, že je mám napsané všechny. Nevidím, co by mělo chybět.
What does a drowning number theorist say?
'log log log log ...'
Offline
#16 02. 12. 2011 15:48
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
Počet ekvivalencí odpovídá příslušnému Bellovu číslu
Offline
#18 02. 12. 2011 15:53
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ Andrejka3:
Pokud budou počty prvků v třídě ekvivalence {1,1,1,1}, tak taková ekvivalence bude jedna. Podobně pro následující počty prvků v třídách ekvivalence:
{1,1,2} – 6
{2,2} – 3
{3,1} – 4
{4} – 1
Celkem tedy 1+6+3+4+1=15. Která ti chybí? :-)
Offline
#19 02. 12. 2011 15:55 — Editoval Andrejka3 (02. 12. 2011 16:00)
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ Pavel Brožek:
Nevím. Příšera jedna mi to zhatila. :(
{2,2} nebo {3,1}
Spise {3,1}, v tretim patre, se tremi nulami...
What does a drowning number theorist say?
'log log log log ...'
Offline
#20 02. 12. 2011 15:59
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
Už jsem ji našel. Tahle:  :-)
:-)
Offline
#21 02. 12. 2011 16:03
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
↑ Pavel Brožek:
Hurá. Ta mi ale popírá vysněné ideje o nějakých symetriích :D
Tak si to nakreslím znovu. A budu jezdit po cestičkách.
Mimochodem, tento příklad má dvě hvězdičky. Jedna hvězdička nejspíš znamená, že se člověk musí trochu zamyslet. Co znamenají dvě hvězdičky podle autora, to se ještě podívám :-)
What does a drowning number theorist say?
'log log log log ...'
Offline
#22 02. 12. 2011 16:40 — Editoval Andrejka3 (02. 12. 2011 16:44)
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
Doplnila jsem chybějící ekvivalenci. Z každého prvku v druhém patře jdou 3 ručičky nahoru :) za prvky z třetího patra.
Cituji ze sbírky: "Dvojhvězdičkové úlohy pak mohou být pro dobré studenty výzvou k otestování svých znalostí."
What does a drowning number theorist say?
'log log log log ...'
Offline
#23 02. 12. 2011 17:10 — Editoval Andrejka3 (02. 12. 2011 17:13)
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
Příkladem jednoho ze čtyřprvkových generátorů je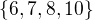 Pak totiz je:
Pak totiz je:
A co dál? Pojďme teď na pětiprvkovou. :D
What does a drowning number theorist say?
'log log log log ...'
Offline
#24 02. 12. 2011 18:04 — Editoval Pavel Brožek (02. 12. 2011 18:17)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
Omlouvám se, že se ještě vracím na začátek, snažím se pochopit zadání, takže jsem zatím ostatní příspěvky moc nečetl.
Nedaří se mi dokázat, že  odpovídá supremu, konkrétně to, že z
odpovídá supremu, konkrétně to, že z  a
a  plyne
plyne 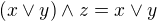 (tedy že
(tedy že 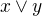 je nejmenší horní závora). Není ještě potřeba distributivita operací
je nejmenší horní závora). Není ještě potřeba distributivita operací 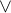 a
a 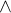 ?
?
Edit: Mám na mysli obecné operace 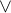 a
a 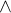 na svazu.
na svazu.
Offline
#25 02. 12. 2011 18:13
Re: Nejmenší generátor svazu ekvivalencí konečné množiny
Příklady generátorů se 4 ekvivalencemi (našel jsem jich 50):
Code:
210|||3 ** 310||2| ** 320|1|| ** 0|321|| 210|||3 ** 310||2| ** 20|31|| ** 30|21|| 210|||3 ** 310||2| ** 20|31|| ** 0|1|32| 210|||3 ** 310||2| ** 30|21|| ** 0|1|32| 210|||3 ** 10||32| ** 320|1|| ** 30|21|| 210|||3 ** 10||32| ** 320|1|| ** 0|31|2| 210|||3 ** 10||32| ** 20|31|| ** 0|321|| 210|||3 ** 10||32| ** 20|31|| ** 30|1|2| 210|||3 ** 10||32| ** 30|21|| ** 0|31|2| 210|||3 ** 10||32| ** 30|1|2| ** 0|321|| 210|||3 ** 320|1|| ** 30|21|| ** 0|31|2| 210|||3 ** 20|31|| ** 30|21|| ** 0|1|32| 210|||3 ** 20|31|| ** 30|1|2| ** 0|321|| 210|||3 ** 30|1|2| ** 0|31|2| ** 0|1|32| 310||2| ** 10||32| ** 320|1|| ** 20|31|| 310||2| ** 10||32| ** 320|1|| ** 0|21||3 310||2| ** 10||32| ** 20|31|| ** 0|21||3 310||2| ** 10||32| ** 20|1||3 ** 30|21|| 310||2| ** 10||32| ** 20|1||3 ** 0|321|| 310||2| ** 10||32| ** 30|21|| ** 0|321|| 310||2| ** 320|1|| ** 20|31|| ** 0|21||3 310||2| ** 20|31|| ** 30|21|| ** 0|1|32| 310||2| ** 20|1||3 ** 30|21|| ** 0|321|| 310||2| ** 20|1||3 ** 0|21||3 ** 0|1|32| 10||32| ** 320|1|| ** 20|31|| ** 0|21||3 10||32| ** 320|1|| ** 30|21|| ** 0|31|2| 10||32| ** 20|31|| ** 30|1|2| ** 0|321|| 10||32| ** 20|1||3 ** 30|21|| ** 0|321|| 10||32| ** 20|1||3 ** 30|1|2| ** 0|21||3 10||32| ** 20|1||3 ** 0|21||3 ** 0|31|2| 10||32| ** 20|1||3 ** 30|1|2| ** 0|31|2| 10||32| ** 30|1|2| ** 0|21||3 ** 0|31|2| 10||2|3 ** 320|1|| ** 20|31|| ** 30|21|| 10||2|3 ** 320|1|| ** 20|31|| ** 0|321|| 10||2|3 ** 320|1|| ** 30|21|| ** 0|321|| 10||2|3 ** 320|1|| ** 0|21||3 ** 0|31|2| 10||2|3 ** 20|31|| ** 30|21|| ** 0|321|| 10||2|3 ** 20|31|| ** 30|1|2| ** 0|21||3 10||2|3 ** 20|31|| ** 0|21||3 ** 0|1|32| 10||2|3 ** 20|31|| ** 30|1|2| ** 0|1|32| 10||2|3 ** 20|1||3 ** 30|21|| ** 0|31|2| 10||2|3 ** 20|1||3 ** 30|21|| ** 0|1|32| 10||2|3 ** 20|1||3 ** 30|1|2| ** 0|321|| 10||2|3 ** 20|1||3 ** 0|31|2| ** 0|1|32| 10||2|3 ** 30|21|| ** 0|31|2| ** 0|1|32| 10||2|3 ** 30|1|2| ** 0|21||3 ** 0|1|32| 320|1|| ** 20|31|| ** 30|21|| ** 0|321|| 20|31|| ** 30|1|2| ** 0|21||3 ** 0|1|32| 20|1||3 ** 30|21|| ** 0|31|2| ** 0|1|32| 20|1||3 ** 30|1|2| ** 0|21||3 ** 0|31|2|
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nejmenší generátor svazu ekvivalencí konečné množiny (TOTO TÉMA JE VYŘEŠENÉ)
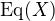 je množina všech ekvivalencí na
je množina všech ekvivalencí na 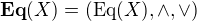 je svaz.
je svaz.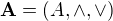 je algebra typu (2,2), kde její binární operace mají následující vlastnosti:
je algebra typu (2,2), kde její binární operace mají následující vlastnosti: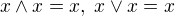

 svaz a definujeme-li na A relaci
svaz a definujeme-li na A relaci 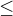 takto:
takto: , pak
, pak 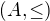 je svazově uspořádaná množina. Dá se pak pomocí vlastností svazu dokázat, že operace
je svazově uspořádaná množina. Dá se pak pomocí vlastností svazu dokázat, že operace 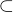 (neostrá). Množina
(neostrá). Množina 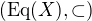 je svazově uspořádaná. Pokud ji chci převést ekvivalentně na svaz, jak je v zadání příkladu, pak odpovídající operace jsou
je svazově uspořádaná. Pokud ji chci převést ekvivalentně na svaz, jak je v zadání příkladu, pak odpovídající operace jsou 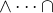 a složitěji
a složitěji 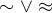 odpovídá průniku všech ekvivalencí na
odpovídá průniku všech ekvivalencí na 
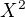 . Tam jsem se ztratila hned na začátku, mám problémy se zápisem.
. Tam jsem se ztratila hned na začátku, mám problémy se zápisem.














 nebo
nebo 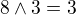 nebo
nebo 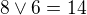 .
. 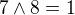 ,
, 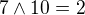 ,
, 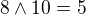 ,
,  ,
, 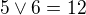 ,
, 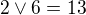 ,
, 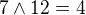 ,
, 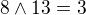 ,
, 