Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 12. 2011 16:56
Limita
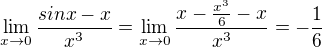
Takhle to vychází :) Jak se dá ale poznat, jak velký tayloří rozvoj použít?
↑↑ halogan:
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#3 02. 12. 2011 17:38 — Editoval FailED (02. 12. 2011 17:41)
Re: Limita
↑ Alivendes:
Když chceš počítat jen s několika členy, měl bys nějak odhadnout chybu, aspoň takhle: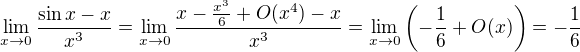
Offline
#5 02. 12. 2011 17:43 — Editoval halogan (02. 12. 2011 17:43)
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita
1) Je třeba tam vkládat i ten zbytkový člen (už neznám přesně terminologii). Jinak to neplatí.
2) Řád poznáš podle toho, jaký pak budeš potřebovat :-) Pokud třeba násobíš/skládáš více funkcí, rozvíjíš je tak, abys pak měl dostatečně vysokou mocninu x, když budeš třeba krátit se jmenovatelem.
U těchto základních limit tedy platí, že ten zbytkový člen musí být tak malý, aby byl řádově menší než jmenovatel. Abys to pak při rozdělení na součet limit dostal do nuly.
Edit: kolega FailED vypsal, co jsem měl na mysli.
Offline
#6 03. 12. 2011 22:27 — Editoval jarrro (03. 12. 2011 22:27)
Re: Limita
↑ Alivendes:myslel som to tak,že keby si v tejto konkrétnej limite použil viac členov tak by si to vedel rozdeliť na súčet polynómu a zlomku a úplne najlepšie je to tam dať celé ako píše FailED
MATH IS THE BEST!!!
Offline