Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s nekonečnem (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 12. 2011 11:35
- miminko.alidgy

- Příspěvky: 114
- Reputace: 4
limita s nekonečnem
Zdravím. Prosím jak je možné, že lim x jdoucí k nekonečnu 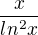 = nekonečno? Vždyť nekonečno/nekonečno je neurčitý výraz....nebo je tam výpočet, který nevidím? Děkuji za rady
= nekonečno? Vždyť nekonečno/nekonečno je neurčitý výraz....nebo je tam výpočet, který nevidím? Děkuji za rady
Offline
- (téma jako vyřešené označil(a) miminko.alidgy)
#2 08. 12. 2011 11:42 — Editoval vanok (08. 12. 2011 11:43)
Re: limita s nekonečnem
Ahoj ↑ miminko.alidgy:,
Vieme ze 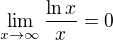
Staci?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 08. 12. 2011 11:51
- miminko.alidgy

- Příspěvky: 114
- Reputace: 4
Re: limita s nekonečnem
↑ vanok:
No právě že když je to 0, tak nechápu, proč je výsledek nekonečno.
Offline
#4 08. 12. 2011 12:00 — Editoval vanok (08. 12. 2011 12:01)
Re: limita s nekonečnem
↑ miminko.alidgy:,
No prave to treba vyuzit na riesenie, ako aj toto: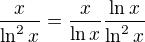
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 08. 12. 2011 13:35
Re: limita s nekonečnem
Ahoj ↑ Rumburak:,
ja som interpretoval 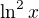 ako
ako 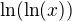
Myslim sa?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 08. 12. 2011 13:43
- miminko.alidgy

- Příspěvky: 114
- Reputace: 4
Re: limita s nekonečnem
↑ Rumburak:
mé zadání je správně napsané, tedy vanok má pravdu.
Offline
#9 08. 12. 2011 14:04
Re: limita s nekonečnem
↑ miminko.alidgy:
O.K. Nepochybuji o tom, žes to napsala správně. Bohužel symbolika nebývá vždy jednotná a jednoznačná.
Například o známých goniometrických vzorcích zapsaných zpravidla ve tvaru
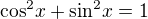 resp.
resp. 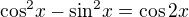
se předpokládá, že budou čteny 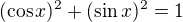 resp.
resp. 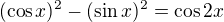
(a NIKOLIV 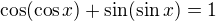 resp.
resp. 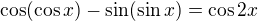 ) .
) .
Proto je v podobných případech dobré význam nejednoznačného symbolu upřesnit s ohledem na kokretní situaci.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s nekonečnem (TOTO TÉMA JE VYŘEŠENÉ)

 je typu
je typu  , což samo o sobě nepomůže. Nebo se pletu ?
, což samo o sobě nepomůže. Nebo se pletu ?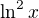 byl
byl  (??)
(??)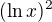 . Tazatelka je myslím dosud "na lajně" (= on line), tak nechť to sama upřesní.
. Tazatelka je myslím dosud "na lajně" (= on line), tak nechť to sama upřesní.