Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 12. 2011 18:36
diskretna !
Ahohjte prosim poradite mi s tymto prikladom dakujem vopred
Číslo 4 môže byť vyjadrené ako súčet jedného alebo viacerých kladných celých číslrl, berúc do úvahy 8 spôsobov, ako poradie:
4 = 1 + 3 = 3 + 1 = 2 + 2 = 1 + 1 + 2 = 1 + 2 + 1 = 2 + 1 + 1 = 1 + 1 + 1 + 1. Všeobecné vzhľadom n ∈ N, vyjadrené ako mnoho spôsobov, ako môžete n?
Offline
#2 09. 12. 2011 18:58 — Editoval standyk (09. 12. 2011 18:58)
Re: diskretna !
↑ katrintn:
Trošku nezrozumiteľné zadanie:
katrintn napsal(a):
Všeobecné vzhľadom n ∈ N, vyjadrené ako mnoho spôsobov, ako môžete n?
Tým myslíš otázku: Ako sa dá všeobecne vyjadriť počet spôsobov vzhľadom na n?
Offline
#4 09. 12. 2011 19:26 — Editoval standyk (09. 12. 2011 20:12)
Re: diskretna !
↑ katrintn:
Treba to rozdeliť na niekoľko častí: konkrétne na n:
1.) ...........: 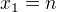 .................... počet spôsobov ako možeme vyrieiť túto rovnicu: je iba jeden spôsob a to že
.................... počet spôsobov ako možeme vyrieiť túto rovnicu: je iba jeden spôsob a to že 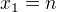
2.) ...........: 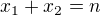 .............. počet spôsobov bude podľa vzorca ktorý máš určite v poznámkach alebo skriptách:
.............. počet spôsobov bude podľa vzorca ktorý máš určite v poznámkach alebo skriptách: 
Tu ale nastáva problém, pretože toto je vzorec na nezáporné riešenia rovnice. My ale potrebujeme kladné riešenie. Preto použijeme substitúciu:  - tým sme dosiahli to že za
- tým sme dosiahli to že za 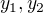 sú už akokeby rezervovaná minimálne jednotka čiže celkové riešenie bude už určite kladné. Správny vzorec na výpočet kladných koreňov tejto rovnice bude teda:
sú už akokeby rezervovaná minimálne jednotka čiže celkové riešenie bude už určite kladné. Správny vzorec na výpočet kladných koreňov tejto rovnice bude teda: 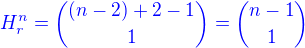
3.) ............... Postupovať budeš podobne ako v prvých dvoch prípadoch: 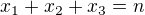
Zavedieš substitúciu a dostávaš 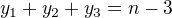 .....
..... 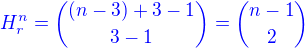
Posldný spôsob bude: 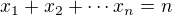 KeĎ urobíš tie kroky čo vyššie dostaneš:
KeĎ urobíš tie kroky čo vyššie dostaneš: 
Ešte je vhodné v tom úuplne prvom kroku ten jeden spôsob si prepísať ako 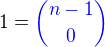
Teraz už len zostáva sčítať tieto disjunktné prípady: 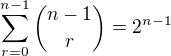
Offline
#6 09. 12. 2011 19:51
Re: diskretna !
↑ katrintn:
čomu konkrétne?
Treba to rozdeliť na n krokov, pretože ten súčet može byť vyjadrený buď ako jedno číslo (4) alebo ako súčet 2 čísel (1+3 , 3+1) alebo ako súčet 3 čísel (1+1+2 , 1+2+1 , 2+1+1) alebo ako súčet 4 čísel (1+1+1+1) a pre každý prípad ratáš osobitne počet možností,
Offline
