Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jádro a ideál v okruhu (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 12. 2011 20:53 — Editoval blb (09. 12. 2011 20:54)
Jádro a ideál v okruhu
Dobrý den,
mám dva okruhy, Z[i] a Z_17, mezi nimi homomorfismus![kopírovat do textarea $\phi: Z[i] \to Z_{17}$](/mathtex/34/34ce8e4c4bead013a9acb1423dbff79e.gif) ,
,
který posílá ![kopírovat do textarea $a + ib \mapsto [a + 4b]_{17}$](/mathtex/f1/f12b00f16602e53db3f2f58b206b8034.gif) .
.
Písmenem i označuju imaginární jednotku, mám ukázat, že jádro  je hlavní ideál (1+4i).
je hlavní ideál (1+4i).
Já jsem ukázal, že ten ideál je podmnožinou jádra, teď nevím, jak na tu druhou část, že v jádru není nic navíc. Prosím o pomoc :-)
Offline
- (téma jako vyřešené označil(a) blb)
#2 09. 12. 2011 21:25
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Jádro a ideál v okruhu
↑ blb:
Ahoj, co je ![kopírovat do textarea $Z[i]$](/mathtex/cb/cbe49179260ad01a1daee925b6d067a0.gif) ? komplexní čísla s celočíselnou reálnou i imaginární částí?
? komplexní čísla s celočíselnou reálnou i imaginární částí?
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 09. 12. 2011 21:29
Re: Jádro a ideál v okruhu
↑ OiBobik:
Zdravím, přesně tak, okruh Z[i] je množina {a + b*i | a,b náleží Z}.
Offline
#4 09. 12. 2011 21:56 — Editoval OiBobik (09. 12. 2011 22:58)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Jádro a ideál v okruhu
↑ blb:
No, tak tu druhou implikaci taky nebude těžké dokázat:
Taktika: zvolíme libovolné číslo 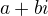 ze
ze ![kopírovat do textarea $Z[i]$](/mathtex/cb/cbe49179260ad01a1daee925b6d067a0.gif) , které posílá zobrazení
, které posílá zobrazení  na
na  , neboli libovolný prvek z jádra. To je ekvivalentní tomu, že
, neboli libovolný prvek z jádra. To je ekvivalentní tomu, že  .
.
No a teď půjde o to, ukázat, že pak nutně existuje komplexní číslo  takové, že
takové, že  , neboli, že
, neboli, že  .
.
Nápověda: v průběhu se bude hodit ukázat, že 
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#5 09. 12. 2011 22:38
Re: Jádro a ideál v okruhu
(x+yi)(1+4i) = x-4y + (y + 4x)i.
Tedy a = x-4y, b = y + 4x.
Vyjádřím y: y = b - 4x;
dosadím do druhé rovnice: x - 4(b-4x) = a; upravím: 17x = a + 4b. Protože a + 4b == 0 mod 17, mohu vydělit. Takže mám x, neznámou y získám z druhé rovnice. Je to takhle OK? Moc děkuju za pomoc :)
Offline
#6 09. 12. 2011 22:45 — Editoval OiBobik (09. 12. 2011 22:48)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Jádro a ideál v okruhu
↑ blb:
Jo, to je ono. Já tam potřeboval tu druhou rovnost modulo vlastně jen proto, že jsem začal vyjadřovat y a ne x, takhle je to jednodušeji formulované.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Jádro a ideál v okruhu (TOTO TÉMA JE VYŘEŠENÉ)