Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 09. 12. 2011 22:09 — Editoval standyk (09. 12. 2011 22:20)
Re: diskretna matematika
↑ katrintn:
Ak správne chápem, tak počet núl v prvých n čísliciach je rovný počtu jednotiek v posledných n čísliciach.
Takto nejak to môže vyzerať._ _ _ _ | _ _ _ _ . Na každej pozícii z prvých n miest môže byť buď 0 alebo 1. to znamená že máme 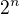 možností. Použijeme identitu:
možností. Použijeme identitu: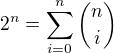
Pre každe kombinačé číslo z tých prvých n číslic ale prislúcha rovnaký počet jednotkových sekvencií v posledných n čísliciach. Je to z dôvodu že používame len číslice 0 a 1 a platí identita 
Čiže pre  núl v prvých n čísliciach bude
núl v prvých n čísliciach bude 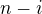 núl v posledných n čísliach. Pre každé kombinačné číslo z tej sumy, ktorú som písal vyššie ale prislúcha rovnaké kombinačné číslo, ktoré hovorí o posledných n čísliciach. Preto, môžeme každé to kombinačné číslo umocniť a všetko sčítať. Dostávame teda:
núl v posledných n čísliach. Pre každé kombinačné číslo z tej sumy, ktorú som písal vyššie ale prislúcha rovnaké kombinačné číslo, ktoré hovorí o posledných n čísliciach. Preto, môžeme každé to kombinačné číslo umocniť a všetko sčítať. Dostávame teda: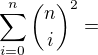
Použijeme kombinatorickú identitu a dostávame: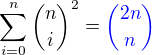
Offline
#4 10. 12. 2011 15:52
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: diskretna matematika
↑ standyk:
Pokud je ono zadání opravdu myšleno tak, jak ho ty chápeš (což souhlasím, že je asi nejpřirozenější výklad), pak lze k výsledku dojít mnohem přímočařeji:
Nechť je v jedné takové uvažované poslouposti celkem k nul mezi prvními n členy. Jelikož uvažujeme posloupnost pouze jedniček a nul, pak je mezi prvními n členy (n-k) jedniček. Podmínka ze zadání nám dává, že v druhé polovině posloupnosti, tj. mezi dalšími n členy, je k jedniček, tedy (n-k) nul. Celkem je tedy v posloupnosti n nul a n jedniček a snadno se rozmyslí, že ať už n jedniček a n nul rozmístíme jakkoli, vždy bude podmínka ze zadání úlohy splněna. Tedy stačí určit počet způsobů rozmístění n nul do posloupnosti 2n čísel (zbylé pozice budou příslušet číslu 1), což je právě  .
.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#5 10. 12. 2011 17:16
Re: diskretna matematika
↑ OiBobik:
Takto priamočiaro ma to teda nenapadlo, aj keď som niečo podobne zčasti tiež použil. Ďakujem :)
Offline