Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál s goniometrickou funkcí (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 12. 2011 18:01 — Editoval Crusad (25. 12. 2011 18:46)
Integrál s goniometrickou funkcí
Zdravím, takže mám zadání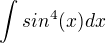
Věděl bych postup přes redukční vzorce, ale nechce se mi je příliš učit, takže jsem šel na to přes substituci  , rozložil jsem to přes parciální zlomky a z prvního zlomku
, rozložil jsem to přes parciální zlomky a z prvního zlomku 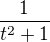 mi vylezl
mi vylezl 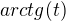 . Problém mám s dalšími zlomky
. Problém mám s dalšími zlomky 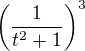 a
a 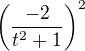 . Zkoušel jsem MAW, ale z toho mi taky nic srozumitelnýho nevylezlo (výsledek ano, ale nějak tak bez postupu).
. Zkoušel jsem MAW, ale z toho mi taky nic srozumitelnýho nevylezlo (výsledek ano, ale nějak tak bez postupu).
Co s tím? Díky za pomoc
Offline
- (téma jako vyřešené označil(a) Crusad)
#2 25. 12. 2011 18:21 — Editoval Phate (25. 12. 2011 18:21)
Re: Integrál s goniometrickou funkcí
to je prave to, ze tg(x) je u tohohle integralu cesta do pekel a jeste hodne trnita. Pokud opravdu chces jit tvou cestou, tak musis pres parcialni zlomky a to u toho na treti uz nebude moc pekny. Jinak redukcni vzorce:
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál s goniometrickou funkcí (TOTO TÉMA JE VYŘEŠENÉ)