Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 12. 2011 17:39 — Editoval Crusad (27. 12. 2011 17:51)
L. transformace impulsu
Prosím o kontrolu, docela se ztrácím v té větě o translaci a hlavně toho výpočtu k ní. Jak se tam přičítá a odčítá, mění znaménka atd., tak se mi často stane, že někde něco zapomenu a protože v zádání písemek není jak, tak jsem si říkal, že se mi to bude lépe integrovat z definice, integrování mi problémy nedělá. Může to takhle být? Možná tam mám někde nějaké špatné znaménko, ale jsem si tímhle postupem o dost jistější.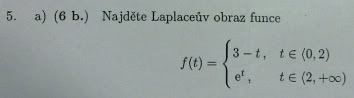

V tom per partes jak se dosazuje nula asi má být 3. 1/-p :)
Offline
#2 27. 12. 2011 19:43
Re: L. transformace impulsu
↑ Crusad: Ahoj, na kontrolu aj toto pomôže...
http://www.wolframalpha.com/input/?i=in … ;t=mfftb01
Offline
#5 27. 12. 2011 21:27
Re: L. transformace impulsu
↑ Crusad:Pekný materiál aj s výpočtami...
http://math.feld.cvut.cz/hyankova/ltru.pdf
Offline
#7 27. 12. 2011 21:43 — Editoval pietro (27. 12. 2011 21:45)
Re: L. transformace impulsu
↑ Crusad: Otestuj si priamo z definicie, ........bez translacie mi zatial vysiel jeden priklad ( z toho co som ti poslal) vobec som nepouzival translaciu ale len Wolframa a zadany tvar impulzu a definiciu...
http://www.wolframalpha.com/input/?i=in … ;t=mfftb01
http://www.wolframalpha.com/input/?i=in … ;t=mfftb01
http://www.wolframalpha.com/input/?i=in … ;t=mfftb01
http://www.wolframalpha.com/input/?i=si … ;t=mfftb01
a dobré je sa naučiť aj tú transláciu asi, ked ju často spomínajú...
Offline
#8 27. 12. 2011 22:03
Re: L. transformace impulsu
Jasně, díky za pomoc. Nějak to tím vychází, ale to exp(t) v tom mém prvním zadání mi teda furt vrtá hlavou. Vyjde tam prostě 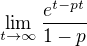 a to podlě mě záleží na hodnotě parametru p. Jednou to je
a to podlě mě záleží na hodnotě parametru p. Jednou to je  a podruhé nekonečno. Tak to nevím jak by se to mělo spočítat.
a podruhé nekonečno. Tak to nevím jak by se to mělo spočítat.
Offline
