Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 12. 2011 17:35 — Editoval Crusad (28. 12. 2011 17:37)
absolutní hodnota
Počítám limitu 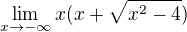 a zůstalo mi
a zůstalo mi 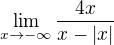 (rozšíření 1 v podobě vnitřku závorky s opačným znaménkem).
(rozšíření 1 v podobě vnitřku závorky s opačným znaménkem).
je správně úprava na 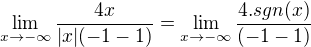 nebo jak se to má jinak zkrátit?
nebo jak se to má jinak zkrátit?
Výsledek původního zadání je podle Wolframu 2.
Snad to je ve správné sekci, jedná se jen o tu úpravu jmenovatele.
Offline
- (téma jako vyřešené označil(a) Crusad)

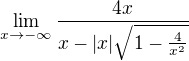 , potom čitatel a jmenovatel vydělím x a dostanu
, potom čitatel a jmenovatel vydělím x a dostanu  .
.