Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 03. 01. 2012 17:58
Re: Gergorinova věta
Ahoj ↑ georgeo4:,
Neviem ake typ pisma pouzivas, ale mne je to necitatelne.
Mozes zmenit ten typ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 03. 01. 2012 19:45 — Editoval vanok (03. 01. 2012 19:51)
Re: Gergorinova věta
↑ georgeo4:,
Ak je to co pises
Najdi Gersgorinove disky matice
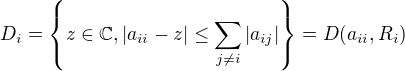
Vlastne hodnoty su v ich sjednoteni
Urob to iste pre transpozovanu maticu
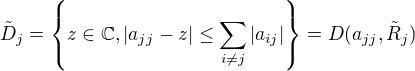
Urob aj tu zjednotenie vsetkych diskov
A na konies mnozina co hladas je priesek tych z jednoteni
PResnejsie bez citania nemozem povedat.
JEdina otazka je ci applikacia na transpozovanu maticu je v tvojich skriptach este v Gersgorinovej vete alebo nie. Ak nie ... taék to prve zjednotenie je odpoved a inteligentne urob poznamku zesa to da zlepsit vdaka ....co som pisal a prieseku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 11. 01. 2013 14:54
- Jirik-1357

- Příspěvky: 30
- Pozice: pracující
- Reputace: 0
Re: Gergorinova věta
vím, že je již toto téma vyřešené, ale taky jsem to hledal a nelazl jsem pěkný odkaz s vysvětlením:
LINEÁRNÍ ALGEBRA, verze 24. 4. 2012, ZDENĚK DOSTÁL, VÍT VONDRÁK
str 191 sekce 23.6, věta 23.7, příklad 23.8
Offline



