Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 09. 01. 2012 16:59
Re: výpočet integrálu
↑ mikrochip:
Souhlasím
↑ Taps:
Možná se ptáš, proč je tomu tak, návod můžeš najít tady Odkaz
Jde o to, že pokud je integrál lichý vzhledem k sinu, použijeme substituci 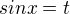
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#4 09. 01. 2012 20:15
Re: výpočet integrálu
↑ Alivendes:
Mohl by mi prosím někdo napsat celý postup ? Po substituci se v příkladu už nějak ztrácím
Offline
#5 09. 01. 2012 23:27 — Editoval Alivendes (11. 01. 2012 21:21)
Re: výpočet integrálu
↑ Taps:
Dobře, nebudeme si lámat hlavu s mezemi, které bychom stejně museli přepočítat nazpět.
Máme řešit integrál:![kopírovat do textarea $\int{\sqrt[5]{sin^2x}.cosxdx}$](/mathtex/f6/f67a2551c56fac22749c4cccd3e3ed3a.gif)
Substituce: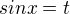
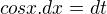
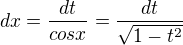
Přejde to na tento integrál:![kopírovat do textarea $\int \sqrt[5]{t^2}.\sqrt{1-t^2}.\frac{dt}{\sqrt{1-t^2}}$](/mathtex/87/8703ea64e867404730787a6655bfa6c8.gif)
![kopírovat do textarea $\int\sqrt[5]{t^2} dt$](/mathtex/80/80d6b0294144f5a87e6a1315c1ed7f19.gif)
Tohle by už neměl být takový problém ...
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#7 11. 01. 2012 20:04
#8 11. 01. 2012 21:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: výpočet integrálu
↑ Taps:
Zdravím,
spíš bych řekla, že Ty jsi zadaní nedopsal (pokud se myslí chybějící x za cos)? Jinak zde substituce 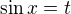 dává hned "kousek původního zadání"
dává hned "kousek původního zadání"  , tedy můžeme rovnou tuto nahradit za dt bez použití
, tedy můžeme rovnou tuto nahradit za dt bez použití 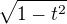 .
.
Je tak vidět? A kde je problém se zadáním? Děkuji.
Offline



