Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Zpětná laplaceova transformace (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 01. 2012 20:44 — Editoval harryharry (17. 01. 2012 20:47)
- harryharry


- Příspěvky: 204
- Reputace: 2
Zpětná laplaceova transformace
Ahoj,
Mám opět problém s řešením, tentokrát bych chtěl jen zkontrolovat myšlenky.
Zadání : Najděte funkci f(t), jejímž Laplaceovým obrazem je funkce:
Psal jsem jen část příkladu, která mi není jasná. Nejsem si jistý hlavně v třetím kroku, dalším úskalím je to, že jsem v kroku 3) prováděl Laplaceovu transtormaci namísto zpětné transformace
“Kde nic není ani smrt nebere.”
Offline
- (téma jako vyřešené označil(a) harryharry)
#2 19. 01. 2012 16:07
Re: Zpětná laplaceova transformace
↑ harryharry: Ahoj, občas pomôže aj
http://www.wolframalpha.com/input/?i=inverse+LT+1%2Fp^2
Offline
#3 19. 01. 2012 16:37
- harryharry


- Příspěvky: 204
- Reputace: 2
Re: Zpětná laplaceova transformace
Wolfram jsem už zkoušel, bohužel mi vyhodil něco nepřehledného.
“Kde nic není ani smrt nebere.”
Offline
#4 19. 01. 2012 19:49
Re: Zpětná laplaceova transformace
↑ harryharry:Tie tri bodky sú tiež funkciou p alebo je to konštanta ?
Offline
#5 19. 01. 2012 20:43 — Editoval harryharry (19. 01. 2012 20:45)
- harryharry


- Příspěvky: 204
- Reputace: 2
Re: Zpětná laplaceova transformace
Nerozumím úplně otázce. Zde mám podobný příklad, píšu ho celý :
Zadání : Najděte funkci f(t), jejímž Laplaceovým obrazem je funkce:
ZLT prvního členu je jasná -> rozklad na parciální zlomky
ale ten druhý mi dělá prostě problém... moje první snaha je vždy násobený zlomek roztrhnout a poté jednotlivě násobit -> LT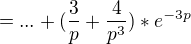
jenže na tento výraz zpětnou laplaceovu transformaci aplikovat neumím
“Kde nic není ani smrt nebere.”
Offline
#6 19. 01. 2012 20:53
Re: Zpětná laplaceova transformace
↑ harryharry: pozri aj transformaciu posunu
http://www.wolframalpha.com/input/?i=in … ;t=mfftb01
Offline
#7 19. 01. 2012 20:58
Re: Zpětná laplaceova transformace
v tabuľke posledná veta o posunutí
http://cs.wikipedia.org/wiki/Laplaceova_transformace
Offline
#8 19. 01. 2012 23:03
- harryharry


- Příspěvky: 204
- Reputace: 2
Re: Zpětná laplaceova transformace
Zase heavisideova funkce. Mohu poprosit o komentář? Nerozumím tomu :-/
“Kde nic není ani smrt nebere.”
Offline
#9 21. 01. 2012 19:00
Re: Zpětná laplaceova transformace
↑ harryharry:
ypsilonové hodnoty tejto klasickej paraboly
http://www.wolframalpha.com/input/?i=pl … ;t=mfftb01
jednoducho prenásobíš posunutou jednotkovou skokovou funkciou (Haeviside step)
http://www.wolframalpha.com/input/?i=pl … ;t=mfftb01
a vlastne tým orežeš pôvodnú parabolu
http://www.wolframalpha.com/input/?i=pl … ;t=mfftb01
Offline
#10 22. 01. 2012 11:08
- harryharry


- Příspěvky: 204
- Reputace: 2
Re: Zpětná laplaceova transformace
Rozumím. Děkuji.
Je to tedy výsledek?
Odkaz
“Kde nic není ani smrt nebere.”
Offline
#11 22. 01. 2012 19:42
Re: Zpětná laplaceova transformace
↑ harryharry: jaké bolo zadanie, netreba to ešte stransformovať integrovať
atp...????
Offline
#12 22. 01. 2012 21:19
- harryharry


- Příspěvky: 204
- Reputace: 2
Re: Zpětná laplaceova transformace
No to se právě ptám. V zadání se po mě chce, abych provedl ZLT, takže  je výsledek, nebo ne?
je výsledek, nebo ne?
“Kde nic není ani smrt nebere.”
Offline
#13 22. 01. 2012 21:46
Re: Zpětná laplaceova transformace
↑ harryharry: o.k. je to to čo máš na začiatku
http://www.wolframalpha.com/input/?i=in … 3D0+to+inf
Offline
#14 23. 01. 2012 13:27
#16 23. 01. 2012 20:56
- harryharry


- Příspěvky: 204
- Reputace: 2
Re: Zpětná laplaceova transformace
Díky Crusad, pomohlo velice!
“Kde nic není ani smrt nebere.”
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Zpětná laplaceova transformace (TOTO TÉMA JE VYŘEŠENÉ)

