Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 30. 01. 2012 09:49
Re: Nalezněte řešení Couchyovy úlohy
↑ jardofpr:
počáteční podm. je x(0)=2
a jak přijdu na to čím rovnici vynásobit?
Offline
#4 30. 01. 2012 10:41
Re: Nalezněte řešení Couchyovy úlohy
↑ jardofpr:
Využívat identitu 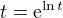 zde ani není nutné . Vynásobíme-li původní rovnici proměnnou
zde ani není nutné . Vynásobíme-li původní rovnici proměnnou  , po úpravě dostaneme
, po úpravě dostaneme ,
,  , atd.
, atd.
Offline
#5 30. 01. 2012 10:46
Re: Nalezněte řešení Couchyovy úlohy
↑ Rumburak:
to je pravda, môže sa stať že potom človek niekedy ale natrafí na príklad keď bude potrebovať celý ten výraz
tu je to ukázané na jednoduchom príklade, možno sa to ľahšie bude pamätať :)
Offline

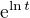

![kopírovat do textarea $\bigg[ x \mathrm{e}^{\ln{t}}\bigg]'=(-1-t^2)\mathrm{e}^{\ln{t}}$](/mathtex/f5/f5af0d32f5b212b05225925c1c7a7eae.gif)