Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 29. 12. 2011 12:36
Re: Grupy
↑ PepaS:
Ahoj, TAKE SLOVA AKO DOBRY DEN? AHOJ ZDRAVIM PROSIM ... nepoznas?
Tvoja otazka sa zda byt mimo kontextu, ak chces odpoved napis presne o co ide, prosim
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 29. 12. 2011 14:33
Re: Grupy
Ahoj poznám, nějak mě to nenapadlo, tak se omlouvám. Ten kontext - do sekce Zajímavé úlohy z algebry jsem dal tuhle, protože si myslím, že může být zajímavá, a připadá mi, že i z algebry. Samozřejmě mě zajímá odpověď, kterou zatím neznám, takže pokud nad tím někdo popřemýšlí, tak to bude fajn. Ale nikoho o to nijak zvlášť neprosím. Pokud to nebylo jasné (není to moc jasné), tak všechna písmenka jsou prvky nějaké grupy, a já se ptám, které grupy tu vlastnost splňují. Jinak přeju dobrý den.
Offline
#4 29. 12. 2011 15:24
Re: Grupy
↑ PepaS:
V prvej casti napriklad

mas ak  ,
,  existuju tak mas okamzite
existuju tak mas okamzite 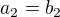
cize tvoje rovnosti nie su mozne pre hocijake parametre 
Posledne dve rovnosti za predpokladu ze  ,
,  existuju
existuju
ti daju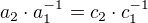
cize 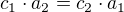
podmienka co musia splnovat parametre 
Pochopitelne, ak tvoja grupa je komutativna, najdes este nejake dalsie relacie... ale aj tak nevidim naco toto moze sluzit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 29. 12. 2011 16:45
Re: Grupy
↑ PepaS:
To mas pravdu, teraz to neplati
ale ta druha relacia 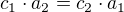 ano.
ano.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 existují x1, x2, y1, y2
existují x1, x2, y1, y2




 .
.