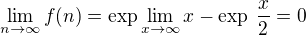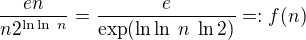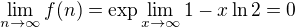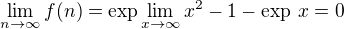Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Asymptotické chování, srovnání několika fcí (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 03. 2012 19:52 — Editoval Andrejka3 (09. 03. 2012 19:55)
Asymptotické chování, srovnání několika fcí
Dobrý den.
Mohl by mi někdo poradit, prosím?
Srovnejte následující fce podle rychlosti růstu (v nekonečnu):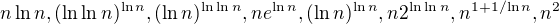 .
.
Ráda bych jako výsledek dostala tabulku, kde by například fce, která by byla výše rostla řádově rychleji než ty níže. A nějak porovnat ty, které rostou podobně rychle.
Určitě je třeba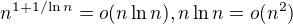 .
.
Navrhuji použít tyto definice:
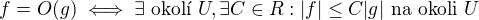
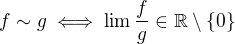
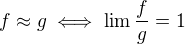 .
.
Moc mi nejde vyšetřit další fce. Schází mi nápady a možná i trochu systém.
Děkuji předem za rady.
edit: jedná se o fce přirozené proměnné, ale to vyjde stejně pro reálnou, že?
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 09. 03. 2012 20:25
Re: Asymptotické chování, srovnání několika fcí
Ahoj ↑ Andrejka3:,
tvoja otazka ma suvis z asymptotickymy rebrikmy porovnania
"échelle de comparaison asymptotique"
A o tom je vela literatury... skus si to najst na google.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 09. 03. 2012 21:16
Re: Asymptotické chování, srovnání několika fcí
↑ Andrejka3:,
jedna z najlepsie napisanych knih, co pise aj o tejto teme je Calcul infinitésimal:Jean Dieudonné .
Ak mozes, skus si ju aspon prelistovat.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 09. 03. 2012 21:23 — Editoval Andrejka3 (09. 03. 2012 21:26)
Re: Asymptotické chování, srovnání několika fcí
↑ vanok:
Bohužel, neumím francouzsky. Ale asi budou překlady - no ne, že bych nějaký na netu našla...
edit: je to tam. Našla, dík.
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 09. 03. 2012 21:59
Re: Asymptotické chování, srovnání několika fcí
↑ Andrejka3:
aha, to si nasla po EN?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 09. 03. 2012 22:41 Příspěvek uživatele Andrejka3 byl skryt uživatelem Andrejka3.
#8 10. 03. 2012 10:23
Re: Asymptotické chování, srovnání několika fcí
Ahoj,
doporučuji si to všechno přepsat na exponenciálu a je to z toho hezky vidět.
Dále pokud je nějaká fce malé o nějaké jiné, tak tím spíše je její velké O.
Offline
#9 10. 03. 2012 10:32
Re: Asymptotické chování, srovnání několika fcí
↑ Mihulik:
Tak například,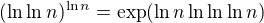 a chci to porovnat s
a chci to porovnat s 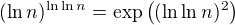 . Teď bych měla porovnat argumenty exp.
. Teď bych měla porovnat argumenty exp.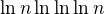 s
s 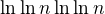 . Co s tím?
. Co s tím?
What does a drowning number theorist say?
'log log log log ...'
Offline
#10 10. 03. 2012 10:52
Re: Asymptotické chování, srovnání několika fcí
No nejrychleji rostoucí člen je zde 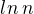 , který se vyskytuje pouze v jednom z výrazů. Navíc je ještě přenásoben něčím, co roste do nekonečna (sice pomalu, ale roste)... formálně z toho uděláš limitu a zjistíš, že
, který se vyskytuje pouze v jednom z výrazů. Navíc je ještě přenásoben něčím, co roste do nekonečna (sice pomalu, ale roste)... formálně z toho uděláš limitu a zjistíš, že 
Offline
#11 10. 03. 2012 11:01 — Editoval Andrejka3 (10. 03. 2012 11:15)
Re: Asymptotické chování, srovnání několika fcí
↑ Mihulik:
A co mohu použít na výpočet té limity, prosím?
Tuším, že použití l'Hospitala přímo by asi nikam nevedlo. Napadá mě zkusit, jestli bude stačit ten nejrychlejší člen na ubití těch dvou ve jmenovateli: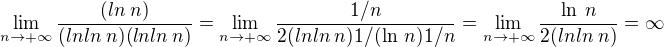 .
.
Aha, děkuji, takže teď když vím, že jeden argument exponenciálny roste řádově rychleji než druhý, měla bych umět odůvodnit, proč i exponenciály dělají totéž. To bych asi zvládla přes nějaká okolí atd. Zkusím přijít na to, jak to udělat jinak...
Díky za rady.
Edit: ne, to stačí tak :)
Takže mám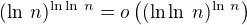
A jestli se nepletu, tak
edit: proč mě ten poslední výsledek tak udivuje...
What does a drowning number theorist say?
'log log log log ...'
Offline
#12 10. 03. 2012 11:11 — Editoval Mihulik (10. 03. 2012 11:14)
Re: Asymptotické chování, srovnání několika fcí
přesně tak:)
A zbytek už je analogický (tu tabulku jsem si taky udělal, takže ti pak když tak můžu pro kontrolu poslat, až to přepíšu...)... navíc se to dá snadno ověřit přes Wolfram;)
Offline
#13 10. 03. 2012 11:14
Re: Asymptotické chování, srovnání několika fcí
↑ Mihulik:
Hurá, dík. Ale bude mi to trvat. :P
What does a drowning number theorist say?
'log log log log ...'
Offline
#15 11. 03. 2012 17:51 — Editoval Andrejka3 (23. 02. 2014 14:29)
Re: Asymptotické chování, srovnání několika fcí
Tabulka podle rychlosti růstu v nekonečnu. Fce, která je níže v tabulce je malé o funkce, která je výše (nahoře rostou rychleji).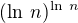


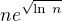
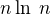



Limity
(1) 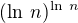 ,
, 
(2)
 ,
, 
(3)
 ,
, 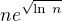
(4)
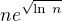 ,
, 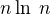
(5)
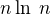 ,
, 
(6)
 ,
, 
(7)
 ,
, 
Edit: Vrátila jsem se k tomu o několik století později. Teď mě pořadí vyšlo takhle (a počítala jsem jiným způsobem, ale taky vše převedeno nejdříve na exp):
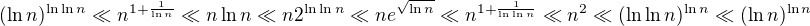 .
. What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Asymptotické chování, srovnání několika fcí (TOTO TÉMA JE VYŘEŠENÉ)

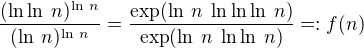
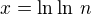
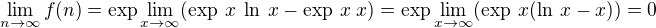 .
.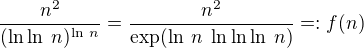
 .
. 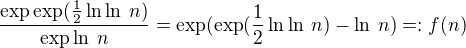
 .
.