Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 14. 03. 2012 22:08
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analytická geometrie č.2
Opět děkuji, postup se mi také jeví v pořádku, jen se mi nezdá dobrý výpočet pro vyjádření y:
nemá tam být 2I-5II, můžeš překontrolovat např. dosazením bodu pro z=0, ostatní souřadnice si dopočti, bod musí splňovat rovnice každé z rovin.
Offline
#6 15. 03. 2012 00:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analytická geometrie č.2
ano, po opravě (př. 4) je to v pořádku.
b) tady se mi nedá  v čitateli - jak vzniklo?
v čitateli - jak vzniklo? 
c) tudíž to znamená, že společný bod má souřadnice z=0, x, y - dopočti dosazením t=0 do parametrického zápisu přímky
Offline



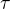










 /:(-3)
/:(-3)
 /:(-1)
/:(-1)


 /:(-1)
/:(-1)
















