Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 14. 03. 2012 11:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analytická geometrie č.1
Zdravím,
máš to hezky naTeXováno, ale dost neprůhledně, jakou pomoc potřebuješ? Je to Tvůj návrh k řešení:
a pak buď
nebo
Pokud jsem správně pochopila zápis, navrhuješ ověřovat, zda je přímka rovnoběžná s rovinou nebo zdá přímka a rovina mají společný bod Q a potom lze také stanovit odchylku přímky od roviny? Ano, je to vhodná cesta. V čem je tedy problém (obdobně upřesní, prosím, také v Tvém 2. tématu)? Děkuji.
Offline
#3 14. 03. 2012 17:41
Re: Analytická geometrie č.1
↑ jelena:
Tak se mi podařilo tento příklad vypočítat, avšak bych potřeboval výsledek ověřit, zda jsem správně postupoval.
Vypočetl jsem si směrový vektor  .
.
Z toho zjistím parametrickou rovnici přímky p: 


Pak jsem si udělal z parametrické rovnice obecnou rovnici:


_____________________

______________________

Pak jsem dosadil par. výrazy přímky do obecné rovnice roviny.

![kopírovat do textarea $\Rightarrow Q[\frac{13}{5};-\frac{9}{5};-\frac{1}{5}]$](/mathtex/4a/4adb4502fb829045d4361d9ebc5ce879.gif)
Offline
#4 14. 03. 2012 21:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analytická geometrie č.1
↑ tesarin:
děkuji, úplně přesně (co do číselných výpočtů) jsem nekontrolovala, ale postup vypadá v pořádku.
Offline
 a roviny
a roviny 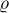 , je-li
, je-li ![kopírovat do textarea $A [2;-3;-2]$](/mathtex/66/660ea97d35001609a6187a09d4fe6b04.gif) ,
, ![kopírovat do textarea $B [3;-1;1]$](/mathtex/a0/a01d9372857e1f92d72a096ff41010a0.gif) a
a 








![kopírovat do textarea $\Rightarrow Q[1;-5;-5]$](/mathtex/50/5042eecd6ade85cae5041093d30e19e4.gif)
 !
!