Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Mocniny permutace?? (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 03. 2012 22:36 — Editoval slim2303 (14. 03. 2012 23:07)
Mocniny permutace??
Jsou dány permutace  . Platí
. Platí 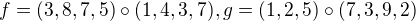 .
.
Zapište permutaci 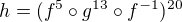 ve tvaru součinu nezávislých cyklů. Permutace h je součinem dvou nezávislých cyklů
ve tvaru součinu nezávislých cyklů. Permutace h je součinem dvou nezávislých cyklů 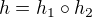 . (Cykly zapisujte ve tvaru "(2,5,7,3)".)
. (Cykly zapisujte ve tvaru "(2,5,7,3)".)
Cyklus 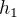 obsahující číslo 1 je: ???
obsahující číslo 1 je: ???
Druhý cyklus 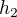 (obsahující 2) je: ???
(obsahující 2) je: ???
Offline
- (téma jako vyřešené označil(a) slim2303)
#2 15. 03. 2012 00:03
Re: Mocniny permutace??
Vyjadri, najprv 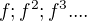
to iste pre 
a urci permutaciu  v zatvorke.
v zatvorke.
A potom a vysetri 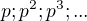
a najdi vyslednu permutaciu.
A dokonci cvicenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 15. 03. 2012 00:38 — Editoval ruamaixanh (15. 03. 2012 00:39)
- ruamaixanh

- Místo: Tachov
- Příspěvky: 100
- Reputace: 11
Re: Mocniny permutace??
Zdravím,
f lze rozložit na 2 komutující cykly:  , a proto f má řád 4; g lze rozložit na
, a proto f má řád 4; g lze rozložit na 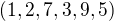 , a proto má řád 6. Hledaný součin bude stejný jako
, a proto má řád 6. Hledaný součin bude stejný jako 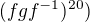 , dále
, dále 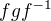 má stejnou strukturu jako
má stejnou strukturu jako  , konkrétně
, konkrétně 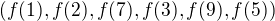 (zkuste to dokázat sám). Stejně jako g tato permutace má také řád 6, a proto musíme vypočítat
(zkuste to dokázat sám). Stejně jako g tato permutace má také řád 6, a proto musíme vypočítat 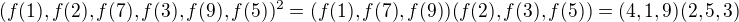 , což je konečný výsledek.
, což je konečný výsledek.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Mocniny permutace?? (TOTO TÉMA JE VYŘEŠENÉ)