Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 03. 2012 10:14
- cyrano52

- Místo: Frýdek-Místek
- Příspěvky: 705
- Škola: VŠB-TUO Ekonomická fakulta
- Pozice: student
- Reputace: 29
Komplexní čísla
Dobrý den, potřeboval bych poradit s tímto příkladem:
Určete, pro která čísla b je komplexní číslo 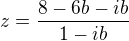
a)reálné b)imaginární c)ryze imaginární
V tomto příkladu si vůbec nevím rady, jak postupovat, ale řekl bych, že by stačilo mi jen poradit začátek. Díky :)
Největší bohatství je vzdělání - R. Kiyosaki
Offline
- (téma jako vyřešené označil(a) cyrano52)
#2 31. 03. 2012 10:22
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Komplexní čísla
Ahoj.
Komplexní číslo má reálnou složku a imaginární.
Označím to číslo z=a+bi, a je reálná část, b imaginární
Pokud je a=0, je číslo ryze imaginární, pokud b=0 je reálné. Pokud jsou a,b nenulové, jedná se o obyčejné imaginární číslo.
Klíčové je tedy upravit na tvar a+bi
Offline
#3 31. 03. 2012 10:43
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Komplexní čísla
↑ cyrano52:
Ještě malá nápověda:
Rozšiř číslo z výrazem 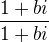
Dále využij toho, že 
Po rozšíření zlomku dej k sobě reálnou část a imaginární část a zjisti dále co po tobě chtějí.
Nikdo není dokonalý
Offline
#4 31. 03. 2012 12:26 — Editoval peter_4 (31. 03. 2012 16:04)
Re: Komplexní čísla
Moc nechápu, jak může někdo říct, že hledá, kdy je komplexní číslo b) imaginární c) ryze imaginárn.
Pokud vím, tak číslo složené z reálného a imaginárního čísla se jmenuje číslo komplexní, né imaginární.
Takže v tom zadání má správně stát a) racionální b) komplexní c) imaginární
(tady taky moc nechápu proč komplexní číslo se na jednu stranu označuje, že je ryze imaginární a na druhou stranu se neříká "ryze racionální", protože ta logika je naprosto stejná)
Jinak kdyby tě zajímalo co je to imaginární číslo tak to vychází z druhých mocnin.
Mocniny jsou čísla, která mají svůj "základ" a svůj "exponent"
a^b=c; např. 3^2=9
O číslu "c" řeknu, že je "mocnina" o číslu "a", že je "základ" dané mocniny a o číslu "b", že je exponent mocniny.
Pokud budu hledat základ od druhé mocniny 9, tak k tomu se používá druhá odmocnina(hledání druhého základu).
Platí jedno důležité pravidlo, že pokud je mocnina složena z násobků, tak základ lze najít tak, že se najdou základy jednotlivých násobků a ty se pak mezi sebou vynásobí.
Např. 
Stejně tak pokud se hledá základ od mocniny, který vznikne podílem dvou čísel...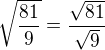
_________________________________________________________________________
(+3)^2=+9; (-3)^2=+9
Platí, že pokud se základ "+3" povýší na druhou mocninu, tak vznikne druhá mocnina +9
Taky platí, že pokud se základ "-3" povýší na druhou mocninu, tak vznikne druhá mocnina +9
Tedy druhý základ od +9 je jak +3 tak -3. Zároveň je vidět, že umocňováním kladného i záporného čísla vznikne číslo kladné.
Pro představu lze nyní říct, že hledání druhého základu je hledání čísla, které znásobeno sebou samým dá přesně druhou mocninu.
Pokud budu hledat druhý základ od -9  pak nastane celkem velký problém, jelikož neexistuje žádné číslo, od kterého druhá mocnina je záporné číslo, jelikož jak bylo ukázáno výš, tak druhá mocnina od základu +3 i -3 je +9.
pak nastane celkem velký problém, jelikož neexistuje žádné číslo, od kterého druhá mocnina je záporné číslo, jelikož jak bylo ukázáno výš, tak druhá mocnina od základu +3 i -3 je +9.
Je tedy jasné, že druhý základ(nebo taky druhá odmocnina) od negativního čísla nemůže být ani pozitivní číslo ani negativní číslo. Hledaný základ tedy musí patřit k naprosto odlišné skupině čísel, jelikož jej nejde zařadit ani mezi pozitivní(kladná) ani mezi negativní(záporná) čísla.
Kladná čísla jsou větší než "nic"(nula) a záporná jsou menší než "nic", cokoliv je větší než 0 je zařazeno mezi kladná čísla, cokoliv je menší než nula je zařazeno mezi záporná čísla. Takovýto základ tedy není ani větší ani menší než nic. Taky nemůže být 0, jelikož produkt z násobení 0*0 je roven 0, tedy nikoliv zápornému číslu.
A jelikož jakékoliv "možné" číslo musí být buď větší než nula nebo menší než nula, nebo nula samotná, tak druhý základ od záporného čísla nejde zařadit do "možných" čísel, musíme tedy říct, že množství, které představuje takovýto základ "není možné". Což vede k myšlence čísel, která nejsou možná. Proto takováto čísla jsou označována jako "imaginární" jelikož existují pouze v imagination(představě).
Všechny zápisy 

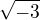
 jsou tedy imaginárními čísly.
jsou tedy imaginárními čísly.
Přestože jde o čísla, která nejsou možná, stále o nich existuje dostatečná představa.
V první řadě, sqrt(-4) je číslo, které znásobeno sebou samým vyprodukuje -4, tedy sqrt(-4)*sqrt(-4)=-4, nebo sqrt(-1)*sqrt(-1)=-1.
Vzhledem k dvěma již výše zmiňovaným pravidlům.
sqrt(-4)*sqrt(-9)=sqrt(-4*-9)=sqrt(36)= násobek dvou imaginárních čísel je tedy číslo reálné
stejně tak sqrt(-4)*sqrt(+9)=sqrt(-36)= násobek reálného a imaginárního čísla je číslo imaginární
(Podobně s podílem sqrt(-4)/sqrt(-9) ...)
Taky platí že sqrt(-1) = jak +sqrt(-1) tak -sqrt(-1)
A konečně taky
sqrt(-9)=sqrt(-1*+9)=sqrt(-1)*sqrt(+9)=sqrt(-1)*3
Z čehož je vidět, že to, proč imaginární čísla nejsou možná lze redukovat na odmocninu(základ) z -1.
Odmocnina z (-1) se označuje jako "i" a komplexní číslo je číslo, které je složené z reálného a imaginárního čísla dohromady. Jak bylo ukázáno sqrt(-1)*sqrt(-1), tedy i*i=-1.
Offline
#5 31. 03. 2012 14:26
- cyrano52

- Místo: Frýdek-Místek
- Příspěvky: 705
- Škola: VŠB-TUO Ekonomická fakulta
- Pozice: student
- Reputace: 29
Re: Komplexní čísla
↑ peter_4:
Díky za obšírné vysvětlení problematiky komplexních čísel, bohužel všechno tohle už vím. :) Ale i tak samozřejmě díky :).
↑ Cheop:↑ Hanis:
Došel jsem k tomuto komplexnímu číslu: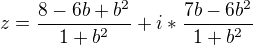
Stanovil jsem rovnici:
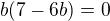
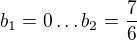
Tj. tedy pro reálné komplexní číslo.
Co se týče imaginárního, je ve výsledku toto: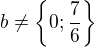
Já si ale myslím, že by tam měla patřit i 2 a 4, protože když dosadíme tyto dvě čísla, dostaneme číslo ryze imaginární. Tak nevím, jestli je chyba ve výsledku, či ve mne :)
Největší bohatství je vzdělání - R. Kiyosaki
Offline
#6 31. 03. 2012 14:47 — Editoval peter_4 (31. 03. 2012 23:23)
Re: Komplexní čísla
Pochybuju, žejsi vůbec věděl, že mocnina má nějaký základ, protože v češtině se to nejen neučí, ale ani to slovo v češtině u mocnin neexistuje.
Taky bych rád upozornil na to, jak jsem napsal výš(ale to ty určo všechno víš :) )... v zadání nemáš napsané, že heldáš "b", které je množinou reálných čísel, a znovu opakuji, že násobek dvou imaginárních čísel je číslo reálné. Čili pokud za "b" dosadíš jakékoliv imaginární číslo, pak "z" bude také komplexní číslo.
Předpokládám, že jsi to tam jen zapomněl napsat a to zadání mělo znít: určete pro která "reaálná čísla" b, je...
Offline
#7 31. 03. 2012 15:02 — Editoval Cheop (31. 03. 2012 15:03)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Komplexní čísla
↑ cyrano52:
Když se bude:
1) b rovnat 0 nebo 7/6 potom bude číslo z reálné
2) b rovnat 2 nebo 4 potom bude číslo z ryze imaginární
3) b různé od 0 nebo od 7/6 nebo od 2 nebo od 4 potom bude číslo z číslem komplexním
Nikdo není dokonalý
Offline
#8 31. 03. 2012 15:24 — Editoval peter_4 (31. 03. 2012 15:34)
Re: Komplexní čísla
Btw to je otázka věcí, pokud řeknu, že reálná čísla jsou ve skutečnosti komplexní bez imaginárního čísla a o imaginárních číslech řeknu, že jsou to čísla komplexní s nulovým reálným číslem, pak samozřejmě oboje můžu označit za čísla komplexní.
Na druhou stranu pokud řeknu, že komplexní číslo, které není složeno z imaginárnícho čísla již není komplexní, pak samozřejmě musím říct, že číslo bez reálného čísla také není číslo komplexní. Bohužel jak jsem psal výš, tak imaginární číslo není ani kladné ani záporné a taky není nula, zatímco reálné číslo nula je...
čili 0*i není imaginární číslo, zatímo 0*jednotka reálné "množství" je.
Předpokládám, že jestli z nějakého důvodu součástí komplexního čísla je i řešení pro 2 a 4, pak je to právě tento.
Offline