Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » parciální derivace podle xy (TOTO TÉMA JE VYŘEŠENÉ)
#2 18. 10. 2008 17:05 — Editoval lukaszh (18. 10. 2008 17:07)
Re: parciální derivace podle xy
↑ Lucky11:
Je daná  , potom
, potom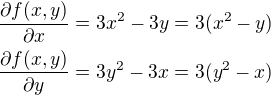
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#4 18. 10. 2008 17:07 — Editoval lukaszh (18. 10. 2008 19:45)
Re: parciální derivace podle xy
↑ Lucky11:
Myslíš deriváciu 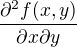
?
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#8 18. 10. 2008 17:18 — Editoval lukaszh (18. 10. 2008 17:19)
Re: parciální derivace podle xy
↑ Lucky11:
Ešte malá poznámka: Je dôležité v akom sú premenné poradí, napríklad derivácia 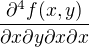
znamená, že funkciu najprv derivuješ podľa x potom podľa y a potom ešte dvakrát podľa x.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#11 18. 10. 2008 21:59
Re: parciální derivace podle xy
↑ Alegory:
A o aký výraz sa jedná?
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#12 18. 10. 2008 22:00
Re: parciální derivace podle xy
Omlouvám se jsem tu poprvé, tak to zkusím ještě jednou...
http://www.sitmo.com/gg/latex/latex2png … ac%7BR%5E2(m_1(g-%5Cfrac%7B2h%7D%7Bt%5E2_1%20%7D)-m_2(g-%5Cfrac%7B2h%7D%7Bt%5E2_2%20%7D))%20%7D%7B2h(%5Cfrac%7B1%7D%7Bt%5E2_1%20%7D-%5Cfrac%7B1%7D%7Bt%5E2_2%20%7D)%7D
Offline
#13 18. 10. 2008 22:03
Re: parciální derivace podle xy
↑ lukaszh:
Bohužel mi to nejde...
Mohu ho ale zaslat na e-mail....
Nerozumím si s touhle technikou :-(
Offline
#14 18. 10. 2008 22:04
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: parciální derivace podle xy
↑ lukaszh:
V mnoha praktických případech ale na pořadí nezáleží (Schwarzova věta).
Offline
#16 18. 10. 2008 22:09
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: parciální derivace podle xy
Nejaky moment setrvacnosti?
Offline
#17 18. 10. 2008 22:10
Re: parciální derivace podle xy
↑ lukaszh:
Je to Výpočet momentu setvačnosti z pohybové rovnice... A parciální derivace potřebuji k určení nejistot.... Bohužel v matematice jsme teprve začali s parciálními derivacemi...:-(((
Offline
#19 18. 10. 2008 22:12
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: parciální derivace podle xy
↑ lukaszh:
Byl jsi navržen a zvolen :-)
Hodne zdaru :-)
Offline
#20 18. 10. 2008 22:13
Re: parciální derivace podle xy
↑ kaja.marik:
jj výpočet momentu setrvačnosti z pohybové rovnice... A parciální derivaci potřebuji k výpočtu nejistot měření, ale bohužel nás parciální derivování učí teprve teď :-(((
Offline
#21 18. 10. 2008 22:22 — Editoval lukaszh (18. 10. 2008 22:35)
Re: parciální derivace podle xy
Úpravami som dostal takýto "škaredý" zlomok:
Mám taký pocit, že tie derivácie budú vyzera? dos? divoko :-)
Podľa t_1: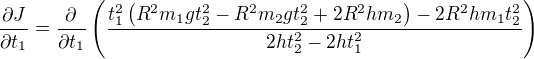
Zavediem substitúciu pre uľahčenie 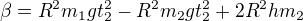

pokračujem...
No a pokračova? nebudem pretože počítač je rýchlejší :-)))
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#22 18. 10. 2008 22:26
Re: parciální derivace podle xy
Jen šílenec by to počítal jinak než pomocí počítače. Dal jsem to do Mathematicy a výsledky jsou takovéto
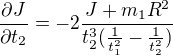
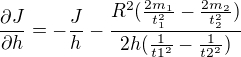
Pokud to ještě někdo počítá, tak se třeba shodneme :-)
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#23 18. 10. 2008 22:27
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: parciální derivace podle xy
Me se derivovat nechce, mozna to ale puvodni tazatel muze spocitat v Maplu, Maxime, Matlabu, .....
A pokud budeme pocitat rucne, tak si vsimneme, ze funkce je jistym zpusobem symetricka: J(m_1,m_2,t_1,t_2,h)=J(m_2,m_1,t_2,t_1,h)
Prehazenim indexu se funkce nezmeni. Az zderivujeme (resp. nekdo zderivuje) podle t_1, staci prohazet indexy a budeme mit derivaci podle t_2.
Takze staci pocitat jenom dve derivace, misto tri.
Offline
#24 18. 10. 2008 22:27
Re: parciální derivace podle xy
↑ lukaszh:
Já vím...:-(
Bohužel jsem na blbé škole kde nám nepomůžou:-((
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » parciální derivace podle xy (TOTO TÉMA JE VYŘEŠENÉ)

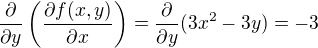
![kopírovat do textarea $J(m_1, m_2,t_1,t_2,h)=\frac{R^2\left[m_1\left(g-\frac{2h}{t^2_1 }\right)-m_2\left(g-\frac{2h}{t^2_2 }\right)\right]}{2h\left(\frac{1}{t^2_1}-\frac{1}{t^2_2 }\right)}$](/mathtex/e5/e56e9f6d18a234811fd718e6621fcb00.gif)