Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 03. 2012 15:20 — Editoval kotry (30. 03. 2012 16:54)
Taylorův polynom
Zdravím, potřeboval bych poradit s těmito příklady. Moc nerozumím tomu zadáni
Př. 1
-nevím co přesně myslí tou druhou řádkou zadání, resp. g(x)= [f(x)]^6 ??????
moje řešení:
f´ (x)= 0 + 2 - 3.(x-1).2= -6x+8 f´ (1)=2
f´´(x)= -6 f´´(1)=-6
T2(x)= 1 + 2.(x-1) + (-6)/(2.1).(x-1)^2 = 1 + 2.(x-1)-3(x-1)^2
Př.2 
- tady vůbec nevím jaký stupeň T.p. mám počítat
- f(0,98) mám dosadit do výsledku a spočítat přesnou hodnotu?? ( =1,98)
moje řešení:
f´ (x)= -(2x-1)e^{2-2x}
f´ (1)=-1
f´´(x)= 4(x-1)e^{2-2x}
f´´ (1)= 0
T2(x)= 2-(x-1)
Offline
- (téma jako vyřešené označil(a) kotry)
#2 30. 03. 2012 15:46 — Editoval Rumburak (30. 03. 2012 16:14)
Re: Taylorův polynom
Ahoj.
K první úloze.
O funkci f víme, že f(1) = 1, f´(1)=2 , f´´(x)= -6 , což je vyčteno z daného T.p. fce f.
K funkci g, o níž víme, že g(x) = [f(x)]^6 , máme sestrojit T.p. (zřejmě stupně 2) , k čemuž budeme vedle g(1) potřebovat čísla g´(1) , g´´(1)
a k jejich výpočtu zase větu o derivaci složené funkce a rovněž větu o derivaci součinu funkcí.
Druhá úloha není na T.p. , ale na diferenciál dy = f'(1) dx , kde dx interpretujeme jako přírůstek proměnné x a dy jako odpovídající přírůstek
proměnné y = f(x).
Offline
#3 30. 03. 2012 17:02
Re: Taylorův polynom
↑ Rumburak:
takže ten první příklad hledám T.p. [(1+2(x-1)-3(x-1)^2] ^6 ???
a ten druhý jen zderivuji a dosadím 0,98 ?
Offline
#5 01. 04. 2012 11:23
#7 01. 04. 2012 11:56 — Editoval vanok (02. 04. 2012 10:47)
Re: Taylorův polynom
Ahoj ↑ kotry:,
Tiez pozdravujem kolegu ↑ Rumburak:
Cvicenie 1. ( pisem cvicenie, lebo priklad je dany vzdy vyrieseny)
Mne sa zda, ze akoze nepozname ani f a ani g...
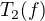
Aritmetika vypoctov na Taylorovych rozvodoch nam umoznuje v polynome
 uvazovat len cleny ktorych typ je konstanta;
uvazovat len cleny ktorych typ je konstanta;  a
a  .
.kontrola
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 02. 04. 2012 10:09 — Editoval Rumburak (02. 04. 2012 10:12)
Re: Taylorův polynom
↑ kotry:
Můj mávrh rozpracoval kolega ↑ jarrro:, jemuž tímto děkuji.
V kontextu s funkcí  platí pro koeficienty T.r. vztahy
platí pro koeficienty T.r. vztahy  , takže T.p. stupně 2 fce
, takže T.p. stupně 2 fce  se středem v 1 bude
se středem v 1 bude
 ,
,
a do toho dosaď za  podle vzorců od ↑ jarrro: a známých hodnot
podle vzorců od ↑ jarrro: a známých hodnot  .
.
Měl by vyjít tentýž výsledek, ke kterému dospěl jinou cestou kolega ↑ vanok: (rovněž zdravím !).
PS. Tu cestu "přes definici" jsem volil s úmyslem, aby sis látku lépe procvičil.
Offline
#11 02. 04. 2012 11:06 — Editoval vanok (02. 04. 2012 11:29)
Re: Taylorův polynom
↑ kotry:,
Vypocet ( v metode co som ti ukazal)je celkom jednoduchy



co ti okamzite da hladany vysledok ( iste si vsimol, ze vo vypocte rozvoju, netreba ho cely pocitat a staci sa limitovat na cleny, ktore nas zaujimaju).
Tiez ti doporucujem, pozorne prestududovat aj metodu kolegu ↑ Rumburak:,
a takto budes mat dobru "kulturu" ako riesit problemy z Taylor-ovymi rozvojmy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 02. 04. 2012 13:05
Re: Taylorův polynom
↑ Rumburak:↑ vanok:
děkuji, už to chápu :-)
(chtělo si to zopakovat kombinační čísla a faktorialy...)
Offline


 exponent v zátvorke je rád derivácie pričom nultá derivácia je samotná funkcia
exponent v zátvorke je rád derivácie pričom nultá derivácia je samotná funkcia

