Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 04. 2012 08:09
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
černá skříňka
Ahoj.
V černé skříňce je schovaný libovolný polynom s přirozenými koeficienty. Vy máte právo na 2 vstupy - 2 čísla, které do polynomu dosadíte a dostanete zpátky funkční hodnoty v těchto bodech.
Vaším úkolem je zjistit, jak tento polynom vypadá :-)
Offline
- (téma jako vyřešené označil(a) Hanis)
#4 05. 04. 2012 14:45 — Editoval BakyX (05. 04. 2012 14:49)
Re: černá skříňka
↑ Hanis:
Čo znamená určiť, ako ten polynóm vyzerá ?
Určiť všetky jeho koeficienty ?
Inak. Stále si neodpovedal, či je to možné :) Na jednoznačné určenie polynómu stupňa  potrebujeme
potrebujeme  funkčných hodnôt.
funkčných hodnôt.
1^6 - 2^6 + 3^6 = 666
Offline
#5 05. 04. 2012 14:59
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: černá skříňka
↑ BakyX:
Ahoj,
Ano, máš určit jeho stupeň a koeficienty.
A ano, jsem přesvědčen o tom, že to lze provést, mi se to zatím vždycky povedlo.
A také souhlasím, že pro určení n-tého stupně je třeba obecně n-funkčních hodnot, ale v tomto případě jsou koeficienty přirozená čísla nebo 0. A taky si po prvním číslu můžeš vzít pauzu a zapřemýšlet, jaké číslo zkusíš potom.
Offline
#6 05. 04. 2012 16:05
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: černá skříňka
↑ Hanis: Co takhle dosadit do polynomu dosadit nějaká ošklivá čísla - třeba pí. Ten polynom nepůjde nijak rozumně zjednodušit (pokud budeme požadovat, aby výstup byla naprosto přesná hodnota), takže koeficienty polynomu snadno odhalíme.
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#7 05. 04. 2012 16:26
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: černá skříňka
↑ Anonymystik:
Dobrá myšlenka, docela jsi mě obehrál :-D
Ale jde to i s dvěma přirozenými čísly.
Offline
#8 05. 04. 2012 17:27 — Editoval Anonymystik (06. 04. 2012 10:34)
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: černá skříňka
↑ Hanis:
Edit: dávám do hidu:
Krásná úloha, velice mě zaujala.
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#9 05. 04. 2012 19:17
Offline
#10 05. 04. 2012 20:26
Re: černá skříňka
↑ Anonymystik:
Mala poznamka:
Miesto  , mozme vybrat hociake cislo
, mozme vybrat hociake cislo 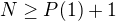 ako basu, a ja by som vybral
ako basu, a ja by som vybral  vo forme
vo forme 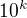 aby ta cierna skrinka pocitala za mna.
aby ta cierna skrinka pocitala za mna.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline