Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 05. 04. 2012 00:35

myrek
Příspěvky: 223
Reputace:   1 
 

matice homomorfismu

dobry den
mam tady prikladek
mam urcit matici homomorfismu f: $U\rightarrow V$ vzhledem k bazim B a C, kde U je $Z^{5}_3$ s bazi B={(2,4,0),(3,1,4),(1,1,0)}, $V=<(3,1,0),(1,2,3)>\subseteq Z^5_3$ s bazi C={(1,2,3),(3,1,2)}
kde f(x,y,z)=(3x+4y+z,x+3y+2z,3y+3z).


takze dela se to tak ze si tam do te prevadeci f dosadim veci z B
tedy dostanu f(2,4,0)=(22,14,12) f(3,1,4)=(17,14,15) f(1,1,0)=(7,4,3) a to dam do matice a je to nebo se mylim a musim delat jeste neco? dekuji

a Dale najdete matici prechodu od baze C k bazi D={(4,3,0),(0,0,1)}

Offline

  • (téma jako vyřešené označil(a) myrek)

#2 05. 04. 2012 02:16

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: matice homomorfismu

Ahoj ↑ myrek:,
Tu som dal odpoved na tvoju poslednu otazku
http://forum.matweb.cz/viewtopic.php?id=38542

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#3 05. 04. 2012 12:43 — Editoval myrek (05. 04. 2012 12:54)

myrek
Příspěvky: 223
Reputace:   1 
 

Re: matice homomorfismu

↑ vanok:
a to predtim mam dobre?
nebo musim pocitat vuci kanonicke bazi?

Offline

 

#4 05. 04. 2012 13:13 — Editoval vanok (05. 04. 2012 13:14)

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: matice homomorfismu

↑ myrek:↑ myrek:
Nie je to dobre,
vypocital obrazy vektorov bazy B
a vysledky co si dostal treba napisat v baze C (podla textu cvicenia), 
Male, ale uzitocne myslienky:

V baze B={b_1(2,4,0),b_2(3,1,4),b_3(1,1,0)}
napriklad b_1 ma suradnice [1;0;0]  (mozes pisat aj  $[1;0;0]_B$ ak by mohli byt pochybnosti).
Cize cely problem je vediet v akej bazy pracujes.

Otazka: Matica co si nasiel je vyjadrena a akych bazach?

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#5 05. 04. 2012 13:38

myrek
Příspěvky: 223
Reputace:   1 
 

Re: matice homomorfismu

↑ vanok:
takze ta matica co tam mam je v bazich BB?

a nebo me napada jeste takovy vztah

a nebo mam $f_{CB}$ urcit pomoci vztahu ze udelam matici inverzni k
1 3
2 1
3 2

vynasobim matici a ted nevim jakou neco jako asi [f]_{K_3 K_2}? prip jak stvorit

a vynasobim matici
2 3 1
4 1 1
0 4 0

Offline

 

#6 05. 04. 2012 14:03

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: matice homomorfismu

↑ myrek:
Nie je to v baze b do standartnej baze.
Pocital si obrazy vektorov baze B. a vysledk je vyjadreny v standarnej  baze .
NA odpoved tejto otazky musis postupne vyjadruit tie obrazy v baze C
Zacni asi takto
f(2,4,0)=(22,14,12)= a(1,2,3)+b(3,1,2) ...urci a; b
...;
poznamka :ked pises

takze ta matica co tam mam je v bazich BB?

je to logicka chyba;
ako chces aby baza 3roj rozmerneho priestoru bola aj baza aj dvojrozmerneho priestoru?

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#7 05. 04. 2012 14:13

myrek
Příspěvky: 223
Reputace:   1 
 

Re: matice homomorfismu

↑ vanok:
takze mam a+3b=22 z toho a=22-3b
2a+b=14 tedy 44-6b+b=14 cili 30=5b tedy b=6
a=4

Offline

 

#8 05. 04. 2012 14:25

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: matice homomorfismu

↑ myrek:↑ myrek:, vsak urob skusku a uvidis§
a potom pokracuj....z druhym vektorom.

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#9 05. 04. 2012 14:34

myrek
Příspěvky: 223
Reputace:   1 
 

Re: matice homomorfismu

↑ vanok:tak ve zkousce mi to pro 3a+2b nevychazi delam nekde chybu? :(

Offline

 

#10 05. 04. 2012 14:50 — Editoval vanok (05. 04. 2012 16:22)

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: matice homomorfismu

↑ myrek:
pokial ti to nevychadza je niekde chyba, ale kde???
Skontroluj tvoje vypocty ( lebo su neuplne, nebral si do uvahy tretiu rovnicu ...a mozna konkluzia moze byt, ze riesenie neexistuje)

kontrola

Autor skryl část textu. Zobrazit/skrýt!


A ak su spravne, tak co to znamena?

Pozor, ale nezabudni ze pracujes v $Z^5$

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#11 05. 04. 2012 15:09 — Editoval myrek (05. 04. 2012 15:19)

myrek
Příspěvky: 223
Reputace:   1 
 

Re: matice homomorfismu

↑ vanok:
mozna uz vim ja se mam pohybovat v podprostore nejakeho Z_5 takze bych ty cisla mel zrejme modulit peti
f(2,4,0)=(2,4,2)
tedy mam a=1 b=2

pro druhy a=3 b=3
pro treti a=0 b=4

zkouska funguje

a to ted dam do matice ty acka a becka a mam matici homomorfismu?

Offline

 

#12 05. 04. 2012 16:03 — Editoval gigo (05. 04. 2012 16:15)

gigo
Příspěvky: 93
Reputace:   0 
 

Re: matice homomorfismu

↑ vanok:↑ myrek:
a co se tyce matice prechodu od C k D neni mi to jasne ptz tu nemam nic ctvercoveho
1 3 | 4 0
2 1 | 3 0
3 2 | 0 1

takto | znacim oddeleni leve a prave strany a sem zvykly na leve strane udelat jednotkovou matici a na prave dostat matici prechodu ale to se tady nepovede takze jak to doplnit nejak

Offline

 

#13 05. 04. 2012 16:18 — Editoval vanok (05. 04. 2012 16:23)

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: matice homomorfismu

↑ gigo:
JA som dal kolegovy len metodu,
↑ vanok:
ale nikde som nevidel ze by urobil vypocet ( ktory je inac velmi jednoduchy).

Treba vediet vyjadrit vektory novej bazy v starej C
C={(1,2,3),(3,1,2)}

D={(4,3,0),(0,0,1)}

Co znamena ze musis hladat a;b; c, d  v $Z^5$ take ze
$ (4,3,0)=a(1,2,3)+b(3,1,2)$
$(0,0,1)=c(1,2,3)+d(3,1,2)$
A ak uvidis ze to nema riesenie,(co je mozne) tak taka matica neexistuje.... levo baza C a baza D nemaju ten isty obal..
a potom mas taketo moznosti: ucitel chcel vidiet vasu reakciu
alebo je chyba v opise cvicenia?

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#14 05. 04. 2012 16:27 — Editoval vanok (05. 04. 2012 16:29)

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: matice homomorfismu

↑ myrek:
Ano to je skoro hladana matica  ( zabudol si jednu cast)

poznamka: uz od sameho zaciatku si  vsetko mohol pisat v $Z^5$
ako napriklad
f(2,4,0)=(22,14,12)=(2;4;2); f(3,1,4)=(17,14,15) f(1,1,0)=(7,4,3)= (2,4,3)
z klasickou dohodou, ze pises prvky v $Z^5$ ako v $Z$ .

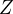Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#15 05. 04. 2012 16:39

gigo
Příspěvky: 93
Reputace:   0 
 

Re: matice homomorfismu

↑ vanok:
aha takze metoda udelat jednotkovou matici ne vzdy vede k reseni ale tato metoda jak vidim vede k reseni
vychazi mi a=1 b=1 c=4 d=2

Offline

 

#16 05. 04. 2012 16:42

myrek
Příspěvky: 223
Reputace:   1 
 

Re: matice homomorfismu

↑ vanok:
na co sem zapomnel jeste
jo mohl ale uplne se mi vytratilo to ze je to v Z_5

Offline

 

#17 05. 04. 2012 16:45

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: matice homomorfismu

↑ myrek:
Prepac, mas to kompletne, to som ja spatne pozeral ( lebo mas vsetky tri obrazy)

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#18 05. 04. 2012 16:48

vanok
Příspěvky: 14600
Reputace:   742 
 

Re: matice homomorfismu

↑ gigo:,
Nerozumiem tvoje vete.
Matica prechodu z jednej bazy do druhej je vzdy matice identickej aplikacii ale vyjadrena v pytanych bazach. ( ak obe bazy su rovnake, tak vtedy a len vtedy,  je to jednotkova matica)

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

#19 05. 04. 2012 16:54

myrek
Příspěvky: 223
Reputace:   1 
 

Re: matice homomorfismu

↑ vanok:
dobre dakujem =)

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson