Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 21. 10. 2008 09:31

Pavel
Místo: Ostrava/Rychvald
Příspěvky: 1828
Škola: OU
Pozice: EkF VŠB-TUO
Reputace:   135 
 

Neomezená funkce

Najděte konečnou funkci definovanou na 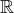$\mathbb R$, která je na libovolném okolí libovolného reálného čísla neomezená.

Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.

Offline

 

#2 21. 10. 2008 11:33 — Editoval BrozekP (21. 10. 2008 11:37)

Pavel Brožek
Místo: Praha
Příspěvky: 5694
Škola: Informatika na MFF UK
Pozice: Student
Reputace:   194 
 

Re: Neomezená funkce

↑ Pavel:

Myslím, že by to měla splňovat obdoba Riemannovy funkce

$R'(x)=\begin{cases} 0 \mbox{ pokud x je iracionalni cislo} \nl q \mbox{ pokud } x=\frac{p}{q} \mbox{, p,q jsou nesoudelna, cela cisla} \end{cases}$

Tím je vyřešen i limes superior v Třinecko - Mostecko Jablunkovské funkci - v každém iracionálním čísle (tedy na množině nenulové Lebesgueovy míry) je limes superior nekonečno.

Offline

 

#3 21. 10. 2008 14:15

Pavel
Místo: Ostrava/Rychvald
Příspěvky: 1828
Škola: OU
Pozice: EkF VŠB-TUO
Reputace:   135 
 

Re: Neomezená funkce

↑ BrozekP:

Výborně, měl to být vlastně i návod k tomu, jak hledat funkci splňující podmínku s limsup.

Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson