Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s eulerovým číslem (TOTO TÉMA JE VYŘEŠENÉ)
#1 11. 04. 2012 21:13
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
limita s eulerovým číslem
chtěl bych se zeptat, jak spočítat limitu: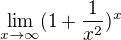
a mělo by to jít spočítat jinak než převodem na exponenciální funkci, došel jsem až sem: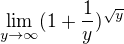
ale dál nevím co s tím
Offline
- (téma jako vyřešené označil(a) Sam_Hawkins)
#3 12. 04. 2012 08:24
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Re: limita s eulerovým číslem
↑ jelena:
aaach děkuji :)
tedy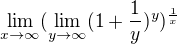
což je
je tak?:)
Offline
#4 12. 04. 2012 09:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita s eulerovým číslem
↑ Sam_Hawkins:
ano, výsledek je dobře, ale nekombinovala bych do toho 2 proměnné (formálně se mi ten zápis nezdá, ale já té formální stránce příliš nerozumím, proto poprosím kolegy o komentář).
Děkuji.
Offline
#5 15. 04. 2012 13:40 — Editoval peter_44 (15. 04. 2012 20:23)
Re: limita s eulerovým číslem
Nevím jestli se ti bude moje řešení líbit Same Hawkinsy, ale limita se dá vyřešit s pomocí zamyšlení se nad binomickou větou
(a+b)^n a toho, jak vznikají příslušné koeficienty, čili například
(a+b)^4 = 1*a*a*a*a + 4*a*b^3+ 6*a^2*b^2 + 4a^3*b + 1*b*b*b*b
(koeficienty jsou 1*, 4*, 6*, 4*, 1*, tedy koeficienty jsou ty čísla co násobí jednotlivé členy binomické věty)
Prakticky jde oto, že násobek vypadá nějak takto
(a+b)*(a+b)*(a+b)*(a+b).... = ...
Koeficienty vznikají tak, kolik možných uspořádání daných písmenek je možné, například pro aaab=>aaab, aaba, abaa, baaa => 4 transpozice, koeficient bude 4*a*b^3.
Není přílíš důležité nějak dál rozvádět tento fakt ani jak vzniká, ikdyž je to poměrně zajimavá věc :).
pro (a+b)^4 => aaaa tedy bude mít koeficient 1, aaab bude mít koeficient 4/1, další členy pak 4*3/2*1, 4*3*2/3*2*1 ...
respektive 1, n/1, n*(n-1)/2*1, n*(n-1)(n-2)/3*2*1
Ty máš 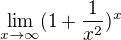
a=1, b=1/(x*x), kde b je velmi malé číslo.
Pokud se do závorky umístí právě ono "b" a to jednou, pak se celý člen zmenší o x*x, zatímco koeficient může přirůst maximálně o jeden násobek "x".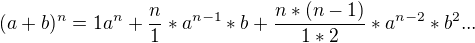
Čímž je vidět, že koeficient přiroste maximálně o *n např. o *(n-1)/2, zatímco do členu přibude *b.
Tedy je jasné, že největší člen bude právě ten, v kterém bude co nejmenší mocnina čísla "b".
Tedy 1^x*b^0 a x*1^(x-1) * b^1
Tedy rozklad těchto dvou členů bude 1 + 1/x, další členy budou už jen menží než člen 1/x,
(špatně) --> vzhledem k tomu, že už jen druhý člen je roven nule, jelikož "x" je nekonečno, nemusíš se dalšíma členama zabývat, výsledek limity je "1"
Offline
#6 15. 04. 2012 14:21
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Re: limita s eulerovým číslem
Hezky, diky za zajimave "alternativni" reseni uvahou, oznacuji tema za vyresene :)
Offline
#8 15. 04. 2012 16:20
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: limita s eulerovým číslem
↑ peter_44:Jen bych upozornil, že věta "druhý člen je roven nule, jelikož "x" je nekonečno, nemusíš se dalšíma členama zabývat" je obecně cestou do pekel, viz třeba
To je součet čísel, kde "už první je nula, protože x je nekonečno", každé další je menší, a přitom ta limita vyjde [budiž ponecháno čtenáři za domácí cvičení].
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#9 15. 04. 2012 20:20 — Editoval peter_44 (15. 04. 2012 23:33)
Re: limita s eulerovým číslem
Jo udělal jsem tam chybu, 1/nekonečno + 1/nekonečno+... a takto nekonečno sčítanců bude rovno 1, proto nejde zanedbat nekonečno opakování, přestože je složeno z nekonečně malých množství.
nicméně...
Pokud si tu posloupnost nahradím a opravdu budu vycházet z toho, že do posloupnosti maximálně přibude *x a podělí se to /x*x pak
toto
(bez toho prvního členu 1*a^n)
Bude určitě menší než toto pokud bude "n" kladné číslo což je: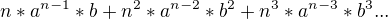
Jak je v zadání a=1 a b=1/x*x a exponent n=x, to pak lze přepsat jako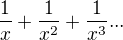
Tato posloupnost vznikne například při dělení 1 mnohočlenem.
Pro b=1 a a=nekonečno je vidět, že tato posloupnost stále bude rovna nule.
Tedy smysl má uvažovat pouze první člen 1*a^n (a=1), což je = 1.
Offline
#10 15. 04. 2012 20:45 — Editoval peter_44 (15. 04. 2012 20:57)
Re: limita s eulerovým číslem
Jinak jestli jsem dobře pochopil zadání té limity cos tu napsal,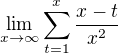


Tyto sčítance jsou zde "x" krát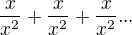

Já si tady namaluju takovou věc (abych ukázal jak sečíst -1-2-3-4-5...)
-1 -2 -3 -4 -5 -6 ...
-6 -5 -4 -3 -2 -1
Říká se tomu triangulární čísla, které vzniknou součtem posloupnosti, která začíná 1čkou a má diferenci 1, v tomto případě -1 a diferenci -1.
Vzhledem k vlastnosti aritmetické posloupnosti a diference je vždy součet krajních členů např. -1 a -6 roven součtu vnitřních např. -2 a -5.
-1 -2 -3 -4 -5 -6 ...
-6 -5 -4 -3 -2 -1
__________________
-7 -7 -7 -7 -7 -7 (tedy počet_členů*-7)
Navíc posloupnost -1-2-3-4... je zde 2krát, součet pro "x" členů je vždy x*(-1-x)/2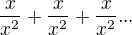
toto bude rovno 1
toto bude rovno
Tedy
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » limita s eulerovým číslem (TOTO TÉMA JE VYŘEŠENÉ)